抛物线有光学性质: 由其焦点射出的光线经抛物线折射后，沿平行于抛物线对称轴的方向射出，今有抛物线y2=2px(p＞0)
一光源在点M(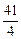
,4)处，由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P，折射后又射向抛物线上的点Q，再折射后，又沿平行于抛物线的轴的方向射出，途中遇到直线l: 2x－4y－17=0上的点N，再折射后又射回点M(如下图所示)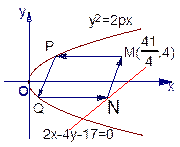
(1)设P、Q两点坐标分别为(x1,y1)、(x2,y2)，证明：y1·y2=－p2；
(2)求抛物线的方程；
(3)试判断在抛物线上是否存在一点，使该点与点M关于PN所在的直线对称？若存在，请求出此点的坐标；若不存在，请说明理由.
试求三直线ax+y+1=0,x+ay+1=0,x+y+a=0构成三角形的条件.
已知A(4，-3)、B(2，-1)和直线l:4x＋3y-2=0，求一点P，使|PA|=|PB|，且点P到直线l的距离等于2.
正方形的中点在原点，若它的一条边所在的直线方程为3x+4y-5=0.求这个正方形的其他边所在的直线的方程.
已知点P(2，-1)，求：
(1)过点P且与原点的距离为2的直线方程；
(2)过点P且与原点的距离最大的直线方程，并求出最大值.
(3)是否存在过点P且与原点的距离为6的直线？若存在，求出该直线的方程；若不存在，请说明理由.
求直线l1:2x+y-4=0关于l:3x+4y-1=0对称的直线l2的方程.