统计表明,某种型号的汽车在匀速行驶中每小时耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为: (
(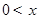 ≤120).已知甲、乙两地相距100千米。
≤120).已知甲、乙两地相距100千米。
(Ⅰ)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(Ⅱ)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
设a,b,c R,a+b+c=0,abc=1.
(1)证明:ab+bc+ca<0;
(2)用max{a,b,c}表示a,b,c中的最大值,证明:max{a,b,c}≥ .
在直角坐标系xOy中,曲线C的参数方程为 (t为参数且t≠1),C与坐标轴交于A、B两点.
(1)求 ;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求直线AB的极坐标方程.
设函数 ,曲线 在点( ,f( ))处的切线与y轴垂直.
(1)求b.
(2)若 有一个绝对值不大于1的零点,证明: 所有零点的绝对值都不大于1.
已知椭圆 的离心率为 , , 分别为 的左、右顶点.
(1)求 的方程;
(2)若点 在 上,点 在直线 上,且 , ,求 的面积.
如图,在长方体 中,点 分别在棱 上,且 , .
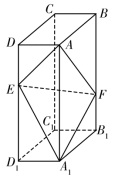
(1)证明:点 在平面 内;
(2)若
,
, 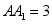 ,求二面角
的正弦值.
,求二面角
的正弦值.