设a,b,c R,a+b+c=0,abc=1.
(1)证明:ab+bc+ca<0;
(2)用max{a,b,c}表示a,b,c中的最大值,证明:max{a,b,c}≥ .
(本小题满分12分)
如图,在六面体ABC-DEFG中,平面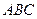 ∥平面
∥平面 ,
,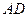 ⊥平面
⊥平面 ,
,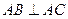 ,
, ,
, ∥
∥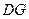 .且
.且 ,
, .
.
(1)求证: ∥平面
∥平面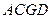 ;
;
(2)求二面角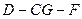 的余弦值.
的余弦值.
(本小题满分10 分)在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且a
分)在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且a =2csinA
=2csinA
(Ⅰ)确定角C的大小:

(Ⅱ)若c=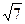 ,且△ABC的面积为
,且△ABC的面积为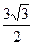
 ,求a+b的值。
,求a+b的值。
已知等比数列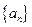 的首项为
的首项为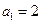 ,公比为
,公比为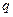 (
(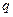 为正整数),且满足
为正整数),且满足 是
是 与
与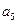 的等差中项;数列
的等差中项;数列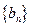 满足
满足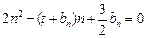 (
(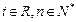 ).
).
(1)求数列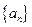 的通项公式;
的通项公式;
(2)试确定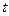 的值,使得数列
的值,使得数列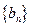 为等差数列;
为等差数列;
(3)当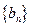 为等差数列时,对任意正整数
为等差数列时,对任意正整数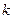 ,在
,在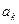 与
与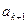 之间插入2共
之间插入2共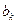 个,得到一个新数列
个,得到一个新数列 .设
.设 是数列
是数列 的前
的前 项和,试求满足
项和,试求满足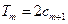 的所有正整数
的所有正整数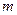 的值。
的值。
在直角坐标系xOy中,椭圆C1: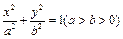 的左、右焦点分别为F1、F2,其中右焦点F2也是拋物线C2:y2 = 4x的焦点,点M为C1与C2在第一象限的交点,且|MF2| =
的左、右焦点分别为F1、F2,其中右焦点F2也是拋物线C2:y2 = 4x的焦点,点M为C1与C2在第一象限的交点,且|MF2| = 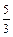 .
.
(1)求椭圆C1的方程;
(2)设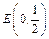 ,是否存在斜率为k (k≠0)的直线l与椭圆C1交于A、B两点,且|AE| = |BE|?若存在,求k的取值范围;若不存在,请说明理由.
,是否存在斜率为k (k≠0)的直线l与椭圆C1交于A、B两点,且|AE| = |BE|?若存在,求k的取值范围;若不存在,请说明理由.
某电视生产企业有A、B两种型号的电视机参加家电下乡活动,若企业投放A、B两种型号电视机的价值分别为a、b万元,则农民购买电视机获得的补贴分别为 万元(m>0且为常数).已知该企业投放总价值为10万元的A、B两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.
万元(m>0且为常数).已知该企业投放总价值为10万元的A、B两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.
(1)请你选择自变量,将这次活动中农民得到的总补贴表示为它的函数,并求其定义域;
(2)求当投放B型电视机的金额为多少万元时,农民得到的总补贴最大?