设二次函数f(x)=ax2+bx+c(a>0),方程f(x)-x=0的两个根x1、x2满足0<x1<x2< 。
。
(1)当x∈[0,x1 时,证明x<f(x)<x1;
时,证明x<f(x)<x1;
(2)设函数f(x)的图像关于直线x=x0对称,证明:x0< 。
。
(本小题满分12分)已知函数 .
.
(1)讨论函数 的单调性;
的单调性;
(2)对于任意正实数 ,不等式
,不等式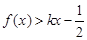 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)是否存在最小的正常数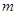 ,使得:当
,使得:当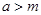 时,对于任意正实数
时,对于任意正实数 ,不等式
,不等式 恒成立?给出你的结论,并说明结论的合理性.
恒成立?给出你的结论,并说明结论的合理性.
(本小题满分12分)已知椭圆 的离心率为
的离心率为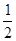 ,椭圆
,椭圆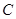 的右焦点
的右焦点 和抛物线
和抛物线
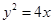 的焦点相同.
的焦点相同.
(1)求椭圆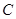 的方程.
的方程.
(2)如图,已知直线
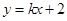 与椭圆
与椭圆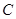 及抛物线
及抛物线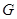 都有两个不同的公共点,且直线
都有两个不同的公共点,且直线 与椭圆
与椭圆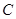 交于
交于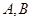 两点;过焦点
两点;过焦点 的直线
的直线 与抛物线
与抛物线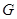 交于
交于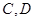 两点,记
两点,记 ,求
,求 的取值范围.
的取值范围.
(本小题满分12分)某校对参加高校自主招生测试的学生进行模拟训练,从中抽出N名学生,其数学成绩的频率分布直方图如图所示.已知成绩在区间[90,100]内的学生人数为2人。
(1)求N的值并估计这次测试数学成绩的平均分和众数;
(2)学校从成绩在[70,100]的三组学生中用分层抽样的方法抽取12名学生进行复试,若成绩在[80,90)这一小组中被抽中的学生实力相当,且能通过复试的概率均为 ,设成绩在[80,90)这一小组中被抽中的学生中能通过复试的人数为
,设成绩在[80,90)这一小组中被抽中的学生中能通过复试的人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)如图,直角梯形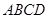 与等腰直角三角形
与等腰直角三角形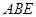 所在的平面互相垂直.
所在的平面互相垂直. ∥
∥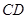 ,
,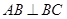 ,
, ,
, .
.
(1)求证: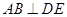 ;
;
(2)求直线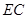 与平面
与平面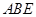 所成角的正弦值;
所成角的正弦值;
(3)线段 上是否存在点
上是否存在点 ,使
,使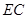 // 平面
// 平面 ?若存在,求出
?若存在,求出 ;若不存在,说明理由.
;若不存在,说明理由.
(本小题满分12分)设等差数列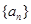 的前
的前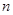 项和为
项和为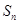 ,且
,且 ,
, ,
,
(1)求等差数列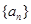 的通项公式
的通项公式 .
.
(2)令 ,数列
,数列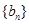 的前
的前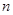 项和为
项和为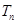 .证明:对任意
.证明:对任意 ,都有
,都有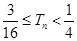 .
.