在锐角△ABC中,求证: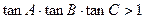 。
。
在△ABC中, ,求
,求 。
。
某酒店根据以往的数据统计发现,在预定了客房的客人中,会有20%的人不出现(即不来入住),所以酒店经常采取超额预定的方式,即预订出去的客房数超出可用客房数,由于超额预定酒店会面临的损失包括:若客人未能如约入住而产生一间空房的话,会造成50元的损失;而已经预定房间的客人由于超额预定而不能得到房间时,宾馆会损失100元(将客人安排到其他宾馆的相关费用),现酒店将5间空房预定给了7位客人,设每位预定客房的客人出现与否是相互独立的. 求7人中恰有2人不出现的概率;
求客人来而没有房住的情况发生的概率;
设
 为酒店的损失,求
为酒店的损失,求 的分布列及数学期望.
的分布列及数学期望.
(参考数据: ,
, ,
, )
)
已知命题 若非
若非 是
是 的充分不必要条件,求
的充分不必要条件,求 的取值范围。
的取值范围。
命题 方程
方程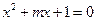 有两个不等的正实数根,命题
有两个不等的正实数根,命题 方程
方程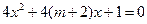 无实数根。若“
无实数根。若“ 或
或 ”为真命题,求
”为真命题,求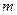 的取值范围。
的取值范围。