已知集合 ,求
,求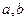 的值
的值
20.(本小题满分16分)
已知函数 .
.
(Ⅰ)若 有两个不同的解,求
有两个不同的解,求 的值;
的值;
(Ⅱ)若当 时,不等式
时,不等式 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(Ⅲ)求 在
在 上的最大值.
上的最大值.
(本小题满分16分)已知椭圆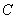 :
: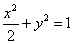 的左、右焦点分别为
的左、右焦点分别为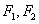 ,下顶点为
,下顶点为 ,点
,点 是椭圆上任一点,⊙
是椭圆上任一点,⊙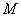 是以
是以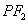 为直径的圆.
为直径的圆.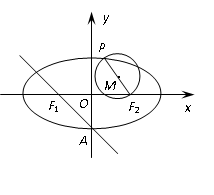
(Ⅰ)当⊙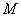 的面积为
的面积为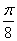 时,求
时,求 所在直线的方程;
所在直线的方程;
(Ⅱ)当⊙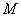 与直线
与直线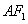 相切时,求⊙
相切时,求⊙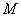 的方程;
的方程;
(Ⅲ)求证:⊙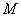 总与某个定圆相切.
总与某个定圆相切.
(本小题满分16分)
某广告公司为2010年上海世博会设计了一种霓虹灯,样式如图中实线部分所示. 其上部分是以 为直径的半圆,点
为直径的半圆,点 为圆心,下部分是以
为圆心,下部分是以 为斜边的等腰直角三角形,
为斜边的等腰直角三角形, 是两根支杆,其中
是两根支杆,其中 米,
米, . 现在弧
. 现在弧 、线段
、线段 与线段
与线段 上装彩灯,在弧
上装彩灯,在弧 、弧
、弧 、线段
、线段 与线段
与线段 上装节能灯. 若每种灯的“心悦效果”均与相应的线段或弧的长度成正比,且彩灯的比例系数为
上装节能灯. 若每种灯的“心悦效果”均与相应的线段或弧的长度成正比,且彩灯的比例系数为 ,节能灯的比例系数为
,节能灯的比例系数为 ,假定该霓虹灯整体的“心悦效果”
,假定该霓虹灯整体的“心悦效果” 是所有灯“心悦效果”的和.
是所有灯“心悦效果”的和.
(Ⅰ)试将 表示为
表示为 的函数;
的函数;
(Ⅱ)试确定当 取何值时,该霓虹灯整体的“心悦效果”最佳?
取何值时,该霓虹灯整体的“心悦效果”最佳?
16.(本小题满分14分)
设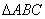 的三个内角
的三个内角 所对的边分别为
所对的边分别为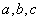 ,且满足
,且满足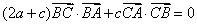 .
.
(Ⅰ)求角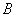 的大小;
的大小;
(Ⅱ)若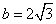 ,试求
,试求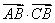 的最小值.
的最小值.
(本小题满分14分)
如图,在直四棱柱 中,
中, ,
,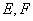 分别是
分别是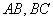 的中点.
的中点.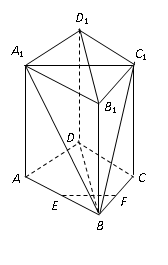
(Ⅰ)求证: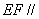 平面
平面 ;
;
(Ⅱ)求证:平面 平面
平面 .
.