如图,已知底角为45°的等腰梯形ABCD,底边BC长为7 cm,腰长为2 cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式,并画出大致图象.
cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式,并画出大致图象.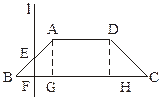
(本小题满分16分)
已知⊙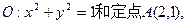 由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足
由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足 (1)求实数a,b间满足的等量关系;(2)求线段PQ长的最小值;
(1)求实数a,b间满足的等量关系;(2)求线段PQ长的最小值;
(3)若以P为圆心所作的⊙P与⊙O有公共点,试求半径最小值时⊙P的方程。
(本小题满分15分)如图所示,在直四棱柱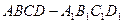 中,
中, ,
,  ,点
,点 是棱
是棱 上一点.(Ⅰ)求证:
上一点.(Ⅰ)求证: 面
面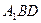 ;(5分)
;(5分)
(Ⅱ)求证: ;(5分)
;(5分)
(Ⅲ)试确定点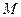 的位置,使得平面
的位置,使得平面
 平面
平面 . (5分)
. (5分)
(本小题满分14分)函数
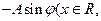
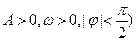 的图象在y轴右侧的第一个最高点(即函数取得最大值的点)为
的图象在y轴右侧的第一个最高点(即函数取得最大值的点)为 ,在原点右侧与x轴的第一个交点为Q(
,在原点右侧与x轴的第一个交点为Q(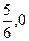 ). 求:(1)函数
). 求:(1)函数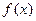 的表达式;(2)函数
的表达式;(2)函数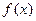 在区间
在区间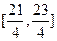 上的对称轴的方程.
上的对称轴的方程.
(坐标系与参数方程)已知直线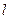 的参数方程:
的参数方程: (
(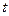 为参数)和圆
为参数)和圆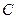 的极坐标方程:
的极坐标方程: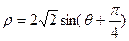 (
(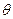 为参数).(1)将直线
为参数).(1)将直线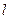 的参数方程和圆
的参数方程和圆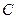 的极坐标方程化为直角坐标方程;(2)判断直线
的极坐标方程化为直角坐标方程;(2)判断直线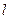 和圆
和圆 的位置关系.
的位置关系.
(几何证明选讲)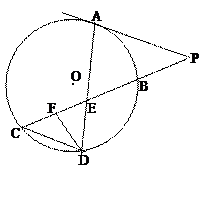
如图所示,已知PA与⊙O相切,A为切点,PBC为割线,,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF·EC.
(1)求证:ÐP=ÐEDF;
(2)求证:CE·EB=EF·EP;
(3)若CE : BE="3" : 2,DE=6,EF= 4,求PA的长.