(13分)如图(3):四面体D—ABC中,DB⊥面ABC, ∠DAB="30°,∠BAC=45°," ∠ACB=90°.BC=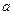 .
.
(1)点A与面BCD的距离; (2)AB与CD成的角的余弦值.
(示范性高中做)
已知正方体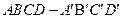 的棱长为1,点
的棱长为1,点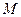 是棱
是棱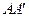 的中点,点
的中点,点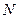 是棱
是棱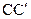 的中点,点
的中点,点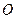 是上底面
是上底面 的中心.
的中心.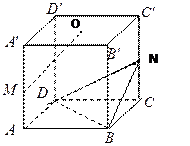 (Ⅰ)求证:MO∥平面NBD;
(Ⅰ)求证:MO∥平面NBD;
(Ⅱ)求二面角 的大小;
的大小;
(Ⅲ)求三棱锥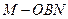 的体积.
的体积.
(本小题共12分)
(普通高中做)
如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AA1=4,点D是AB的中点,
(I)求证:AC⊥BC1;
(II)求证:AC 1//平面CDB1;
(III)求异面直线 AC1与 B1C所成角的余弦值.
(理科做)
甲、乙两队进行一场排球比赛.根据以往经验,单局比赛甲队胜乙队的概率为0.6,本场比赛采用五局三胜制,即先胜三局的队获胜,比赛结束.设各局比赛相互间没有影响.令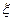 为本场比赛的局数.求
为本场比赛的局数.求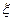 的概率分布和数学期望.(精确到0.0001)
的概率分布和数学期望.(精确到0.0001)
(本小题满分12分)
(文科做)
某商场进行促销活动,促销方案是:顾客每消费100元,便可以获得奖券一张,每张奖券中奖的概率为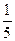 ,若中奖,则商场返还顾客现金100元某顾客购买价格为340元的商品,得到3张奖券(I)求商场恰好返还该顾客现金100元的概率;
,若中奖,则商场返还顾客现金100元某顾客购买价格为340元的商品,得到3张奖券(I)求商场恰好返还该顾客现金100元的概率;
(II)求商场至少返还该顾客现金100元的概率.
(本小题满分12分)
设进入某商场的每一位顾客购买甲种商品的概率是0.5,购买乙种商品的概率是0.6,且购买甲种商品和购买乙种商品是相互独立的,各顾客之间购买商品也是互相独立的.
(Ⅰ)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(Ⅱ)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率.