(理科做)
甲、乙两队进行一场排球比赛.根据以往经验,单局比赛甲队胜乙队的概率为0.6,本场比赛采用五局三胜制,即先胜三局的队获胜,比赛结束.设各局比赛相互间没有影响.令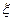 为本场比赛的局数.求
为本场比赛的局数.求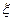 的概率分布和数学期望.(精确到0.0001)
的概率分布和数学期望.(精确到0.0001)
如图,四边形 是正方形,
是正方形,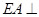 平面
平面 ,
,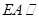
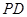 ,
,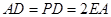 ,
,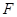 ,
,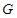 ,
,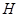 分别为
分别为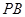 ,
,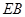 ,
, 的中点.
的中点.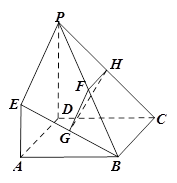
(1)求证: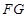
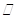 平面
平面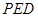 ;
;
(2)求平面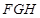 与平面
与平面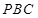 所成锐二面角的大小.
所成锐二面角的大小.
盒子中装有四张大小形状均相同的卡片,卡片上分别标有数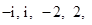 其中
其中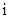 是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响).
是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响).
(1)求事件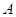 “在一次试验中,得到的数为虚数”的概率
“在一次试验中,得到的数为虚数”的概率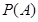 与事件
与事件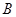 “在四次试验中,
“在四次试验中,
至少有两次得到虚数” 的概率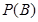 ;
;
(2)在两次试验中,记两次得到的数分别为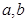 ,求随机变量
,求随机变量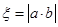 的分布列与数学期望
的分布列与数学期望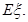
在 中,三个内角
中,三个内角 所对的边分别为
所对的边分别为
 已知
已知 ,
, .
.
(1)求 ;
;
(2)设 求
求 的值.
的值.
已知函数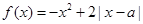 .
.
(Ⅰ)若函数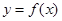 为偶函数,求
为偶函数,求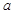 的值;
的值;
(Ⅱ)若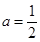 ,求函数
,求函数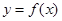 的单调递增区间;
的单调递增区间;
(Ⅲ)当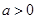 时,若对任意的
时,若对任意的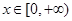 ,不等式
,不等式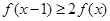 恒成立,求实数
恒成立,求实数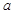 的取值范围.
的取值范围.
已知函数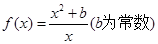 .
.
(Ⅰ)当 ,函数
,函数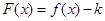 有且仅有一个零点
有且仅有一个零点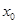 ,且
,且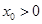 时,求
时,求 的值;
的值;
(Ⅱ)若函数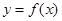 在区间
在区间 上为单调函数,求
上为单调函数,求 的取值范围.
的取值范围.