已知函数 。当
。当 时,函数
时,函数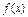 的取值范围恰为
的取值范围恰为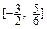 。
。
(1)求函数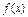 的解析式;
的解析式;
(2)若向量 ,解关于
,解关于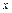 的不等式
的不等式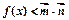 。
。
已知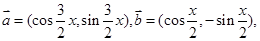 若
若 .
.
(I)求函数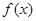 的最小正周期;
的最小正周期;
(II)若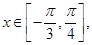 求函数
求函数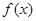 的最大值和最小值.
的最大值和最小值.
已知函数 在[1,+∞)上为增函数,且
在[1,+∞)上为增函数,且 ,
, ,
, ∈R.
∈R.
(1)求θ的值;
(2)若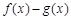 在[1,+∞)上为单调函数,求m的取值范围;
在[1,+∞)上为单调函数,求m的取值范围;
(3)设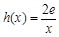 ,若在[1,e]上至少存在一个
,若在[1,e]上至少存在一个 ,使得
,使得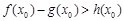 成立,求
成立,求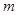 的取值范围.
的取值范围.
已知数列 满足
满足 ,且
,且 ,
,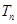 为
为 的前
的前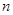 项和.
项和.
(1)求证:数列 是等比数列,并求
是等比数列,并求 的通项公式;
的通项公式;
(2)如果对于任意 ,不等式
,不等式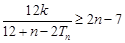 恒成立,求
恒成立,求 实数
实数 的取值范围.
的取值范围.
已知函数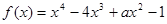 在区间[0,1]上单调递增,在区间[1,2]上单调递减。
在区间[0,1]上单调递增,在区间[1,2]上单调递减。
(1)求 的值;
的值;
(2)若斜率为24的直线是曲线 的切线,求此直线方程;
的切线,求此直线方程;
(3)是否存在实数b,使得函数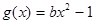 的图象与函数
的图象与函数 的图象恰有2个不同交点?若存在,求出实数b的值;若不存在,试说明理由.
的图象恰有2个不同交点?若存在,求出实数b的值;若不存在,试说明理由.
集合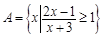 ,
,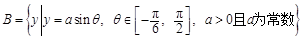 .
.
(1)求集合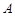 和B;
和B;
(2)若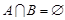 ,求
,求 的取值范围
的取值范围