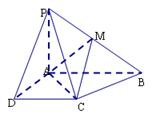
已知如图,四棱锥P-ABCD的底面为直角梯形,AB∥DC, 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=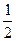 AB=1,M是PB的中点
AB=1,M是PB的中点
(Ⅰ)证明:面PAD⊥面PCD;
(Ⅱ)求AC与PB所成的角;
(Ⅲ)求面AMC与面BMC所成二面角的大小
(本小题满分14分)已知函数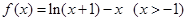 .
.
(1)求 的单调区间;
的单调区间;
(2)已知数列 的通项公式为
的通项公式为 ,求证:
,求证: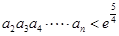 (
( 为自然对数的底数);
为自然对数的底数);
(3)若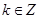 ,且
,且 对任意
对任意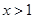 恒成立,求
恒成立,求 的最大值
的最大值
(本小题满分13分)已知等差数列 的前
的前 项和为
项和为 ,并且
,并且 ,
,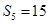 ,数列
,数列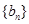 满足:
满足: ,
, ,记数列
,记数列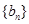 的前
的前 项和为
项和为 .
.
(1)求数列 的通项公式
的通项公式 及前
及前 项和公式
项和公式 ;
;
(2)求数列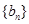 的通项公式
的通项公式 及前
及前 项和公式
项和公式 ;
;
(3)记集合 ,若
,若 的子集个数为16,求实数
的子集个数为16,求实数 的取值范围
的取值范围
(本小题满分12分)已知 的角
的角 所对的边分别是
所对的边分别是 ,设向量
,设向量 ,
,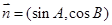 ,
, .
.
(1)若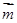 ∥
∥ ,求角B的大小;
,求角B的大小;
(2)若 ,边长
,边长 ,求
,求 的面积的最大值.
的面积的最大值.
(本小题满分12分) 已知函数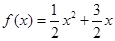 ,,数列
,,数列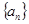 的前
的前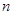 项和为
项和为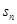 ,点
,点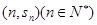 均在函数
均在函数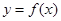 的图象上.
的图象上.
(1)求数列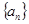 的通项公式
的通项公式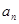 ;
;
(2)令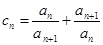 ,证明:
,证明: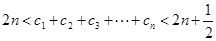 .
.
本小题满分12分)已知集合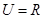 ,集合
,集合 ,函数
,函数 的定义域为集合B.
的定义域为集合B.
(1)若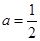 ,求集合
,求集合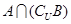 ;
;
(2)命题 ,命题
,命题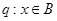 ,若
,若 是
是 的必要条件,求实数
的必要条件,求实数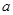 的取值范围.
的取值范围.