通过研究学生的学习行为，专家发现，学生的注意力随着老师讲课时间的变化而变化，讲课开始时，学生的兴趣激增；中间有一段时间，学生的兴趣保持较理想的状态，随后学生的注意力开始分散，设f(t)表示学生注意力随时间t（分钟）的变化规律（f(t)越大，表明学生注意力越集中），经过实验分析得知：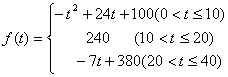
（1）讲课开始后多少分钟，学生的注意力最集中？能持续多少分钟？
（2）讲课开始后5分钟与讲课开始后25分钟比较，何时学生的注意力更集中？
（3）一道数学难题，需要讲解24分钟，并且要求学生的注意力至少达到180，那么经过适当安排，老师能否在学生达到所需的状态下讲授完这道题目？
（本小题满分12分）一个盒子中装有大小相同的2个红球和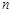
个白球,从中任取2个球.
（Ⅰ）若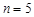
，求取到的2个球恰好是一个红球和一个白球的概率；
（Ⅱ）若取到的2个球中至少有1个红球的概率为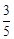
，求.
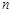（本小题满分12分）已知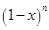
的展开式中第4项与第8项的二项式系数相等.
（Ⅰ）求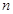
的值；
（Ⅱ）求第4项与第8项的系数之和.
（本小题满分10分）从
名男生和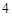
名女生中选出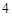人参加学校辩论赛.
（Ⅰ）如果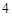人中男生和女生各选
人，有多少种选法？
（Ⅱ）如果男生中的甲和女生中的乙至少有1人在内，有多少种选法？
函数f(x)＝Asin(ωx＋φ)(A>0，ω>0，|φ|<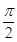
)的一段图象如图所示．
(1)求f(x)的解析式；
(2)求f(x)的单调减区间，并指出f(x)的最大值及取到最大值时x的集合；
(3)把f(x)的图象向左至少平移多少个单位，才能使得到的图象对应的函数为偶函数？
在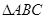
中，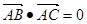
，
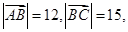
为线段BC的垂直平分线，与BC交与点D，E为上异于D的任意一点，
⑴求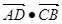
的值。
⑵判断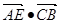
的值是否为一个常数，并说明理由。