抛物线C的方程为 ,过抛物线C上一点P(x0,y0)(x 0≠0)作斜率为k1,k2的两条直线分别交抛物线C于A(x1,y1)B(x2,y2)两点(P,A,B三点互不相同),且满足
,过抛物线C上一点P(x0,y0)(x 0≠0)作斜率为k1,k2的两条直线分别交抛物线C于A(x1,y1)B(x2,y2)两点(P,A,B三点互不相同),且满足 .
.
(Ⅰ)求抛物线C的焦点坐标和准线方程;
(Ⅱ)设直线AB上一点M,满足 ,证明线段PM的中点在y轴上;
,证明线段PM的中点在y轴上;
(Ⅲ)当 =1时,若点P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标
=1时,若点P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标 的取值范围.
的取值范围.
已知中心在原点O,焦点F1、F2在x轴上的椭圆E经过点C(2,2),且抛物线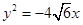 的焦点为F1.
的焦点为F1.
(Ⅰ)求椭圆E的方程;
(Ⅱ)垂直于OC的直线l与椭圆E交于A、B两点,当以AB为直径的圆P与y轴相切时,求直线l的方程和圆P的方程.
如图,在正三棱柱ABC-A1B1C1中,底面ABC为正三角形,M、N、G分别是棱CC1、AB、BC的中点,且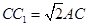 .
.
(Ⅰ)求证:CN∥平面AMB1;
(Ⅱ)求证: B1M⊥平面AMG.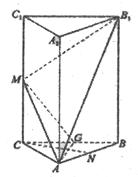
山东省《体育高考方案》于2012年2月份公布,方案要求以学校为单位进行体育测试,某校对高三1班同学按照高考测试项目按百分制进行了预备测试,并对50分以上的成绩进行统计,其频率分布直方图如图所示,若90~100分数段的人数为2人.
(Ⅰ)请估计一下这组数据的平均数M;
(Ⅱ)现根据初赛成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成一个小组.若选出的两人成绩差大于20,则称这两人为“帮扶组”,试求选出的两人为“帮扶组”的概率.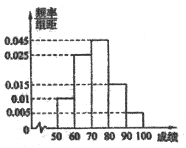
在等差数列{an}中,a1=3,其前n项和为Sn,等比数列{bn}的各项均为正数,b1=1,公比为q,且b2+ S2=12,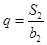 .(Ⅰ)求an与bn;(Ⅱ)设数列{cn}满足
.(Ⅰ)求an与bn;(Ⅱ)设数列{cn}满足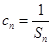 ,求{cn}的前n项和Tn.
,求{cn}的前n项和Tn.
已知△ABC的三个内角A、B、C所对的边分别为a、b、c,向量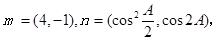

(Ⅰ)求角A的大小;
(Ⅱ)若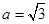 ,试判断b·c取得最大值时△ABC形状.
,试判断b·c取得最大值时△ABC形状.