已知动圆过定点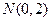 ,且与定直线
,且与定直线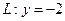 相切.
相切.
(1)求动圆圆心的轨迹C的方程;
(2)若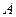 、
、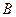 是轨迹C上的两不同动点,且
是轨迹C上的两不同动点,且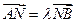 . 分别以
. 分别以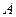 、
、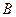 为切点作轨迹C的切线,设其交点Q,证明
为切点作轨迹C的切线,设其交点Q,证明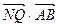 为定值.
为定值.
2010年5月1日,上海世博会将举行,在安全保障方面,警方从武警训练基地挑选防爆警察,从体能、射击、反应三项指标进行检测,如果这三项中至少有两项通过即可入选。假定某基地有4名武警战士(分别记为A、B、C、D)拟参加挑选,且每人能通过体能、射击、反应的概率分别为 。这三项测试能否通过相互之间没有影响。
。这三项测试能否通过相互之间没有影响。求A能够入选的概率;
规定:按人选人数得训练经费(每人选1人,则相应的训练基地得到3000元的训练经费),求该基地得到训练经费的分布列与数学期望。
已知 (其中
(其中 )的最小正周期为
)的最小正周期为 。
。求
 的单调递增区间;
的单调递增区间;在
 中,
中, 分别是角A,B,C的对边,已知
分别是角A,B,C的对边,已知 ,求角C。
,求角C。
定义在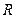 上的函数
上的函数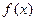 满足
满足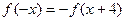 ,当
,当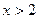 时
时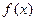 单调递增
单调递增
若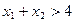 ,且
,且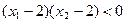 ,判断
,判断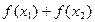 的符号
的符号
(本小题满分12分) 已知函数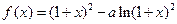 在
在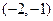 上是增函数,在
上是增函数,在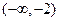 上为减函数.
上为减函数.
(Ⅰ)求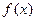 的表达式;
的表达式;
(Ⅱ)若当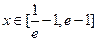 时,不等式
时,不等式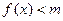 恒成立,求实数
恒成立,求实数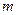 的值;
的值;
(Ⅲ)是否存在实数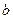 使得关于
使得关于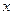 的方程
的方程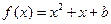 在区间[0,2]上恰好有两个相异的实根,若存在,求实数
在区间[0,2]上恰好有两个相异的实根,若存在,求实数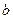 的取值范围.
的取值范围.
(本小题满分12分) 已知双曲线C: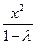
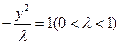 的右焦点为
的右焦点为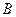 ,过点
,过点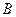 作直线交双曲线C的右支于
作直线交双曲线C的右支于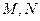 两点,试确定
两点,试确定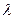 的范围,使以
的范围,使以 为直径的圆过双曲线的中心.
为直径的圆过双曲线的中心.