(本题满分12分) 在九江市教研室组织的一次优秀青年教师联谊活动中,有一个有奖竞猜的环节.主持人准备了A、B两个相互独立的问题,并且宣布:幸运观众答对问题A可获奖金1000元,答对问题B可获奖金2000元,先答哪个题由观众自由选择,但只有第一个问题答对,才能再答第二题,否则终止答题.若你被选为幸运观众,且假设你答对问题A、B的概率分别为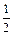 、
、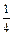 .
.
(1) 记先回答问题A的奖金为随机变量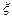 , 则
, 则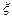 的取值分别是多少?
的取值分别是多少?
(2) 你觉得应先回答哪个问题才能使你获得更多的奖金?请说明理由.
已知数列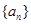 中,
中,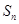 是
是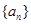 的前
的前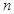 项和,且
项和,且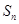 是
是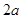 与
与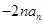 的等差中项,其中
的等差中项,其中 是不等于零的常数.
是不等于零的常数.
(1)求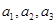 ; (2)猜想
; (2)猜想 的表达式,并用数学归纳法加以证明.
的表达式,并用数学归纳法加以证明.
设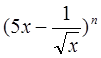 的展开式的各项系数之和为
的展开式的各项系数之和为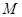 ,二项式系数之和为
,二项式系数之和为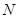 ,
,
若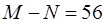 ,(1) 求 n,N,M(2)求展开式中常数项为.
,(1) 求 n,N,M(2)求展开式中常数项为.
用数字0,1,2,3,4,5组成没有重复数字的数.
求:(1)可以组成多少个四位数?
(2)可以组成多少个不同的四位偶数?
(3)可以组成多少个能被5整除的四位数?
已知复数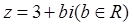 ,且
,且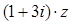 为纯虚数.
为纯虚数.
(1)求复数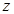 ;(2)若
;(2)若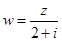 ,求复数
,求复数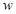 的模
的模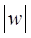
若有穷数列 (
(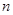 是正整数),满足
是正整数),满足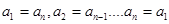 即
即 (
(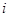 是正整数,且
是正整数,且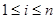 ),就称该数列为“对称数列”。
),就称该数列为“对称数列”。
(1)已知数列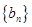 是项数为7的对称数列,且
是项数为7的对称数列,且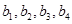 成等差数列,
成等差数列,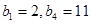 ,试写出
,试写出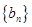 的每一项
的每一项
(2)已知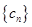 是项数为
是项数为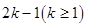 的对称数列,且
的对称数列,且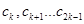 构成首项为50,公差为
构成首项为50,公差为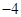 的等差数列,数列
的等差数列,数列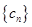 的前
的前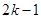 项和为
项和为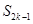 ,则当
,则当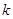 为何值时,
为何值时,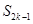 取到最大值?最大值为多少?
取到最大值?最大值为多少?
(3)对于给定的正整数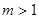 ,试写出所有项数不超过
,试写出所有项数不超过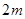 的对称数列,使得
的对称数列,使得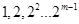 成为数列中的连续项;当
成为数列中的连续项;当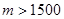 时,试求其中一个数列的前2008项和
时,试求其中一个数列的前2008项和