.如果对任意一个三角形,只要它的三边长a,b,c都在函数f(x)的定义域内,就有f(a),f(b),f(c)也是某个三角形的三边长,则称f(x)为“保三角形函数”.
(1)判断下列函数是不是“保三角形函数”,并证明你的结论:
① f(x)= ; ② g(x)=sinx (x∈(0,π)).
(2)若函数h(x)=lnx (x∈[M,+∞))是保三角形函数,求M的最小值.
【原创】(本小题满分12分)如图,在四面体 中,
中,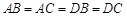 ,点
,点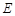 是
是 的中点,点
的中点,点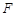 在线段
在线段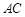 上, 且
上, 且 .
.
(1)若 ∥平面
∥平面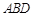 ,求实数
,求实数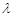 的值;
的值;
(2)求证:平面 平面
平面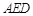 .
.
(本小题满分12分)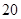 名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.
名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.
(1)求频率分布直方图中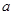 的值;
的值;
(2)分别求出成绩落在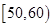 与
与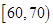 中的学生人数;
中的学生人数;
(3)从成绩在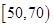 的学生中任选
的学生中任选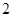 人,求此
人,求此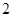 人的成绩都在
人的成绩都在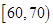 中的概率.
中的概率.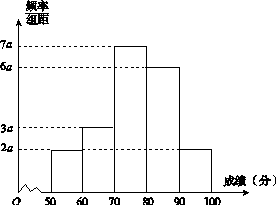
【原创】(本小题满分12分)已知函数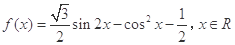 .
.
(1)求函数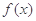 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(2)设△ 的内角
的内角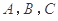 的对边分别为
的对边分别为 且
且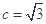 ,
,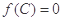 ,若
,若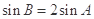 ,求
,求 的值.
的值.
【原创】(本小题满分13分)已知函数 .
.
(1)若f(x)的图象与g(x)的图象所在两条曲线的一个公共点在y轴上,且在该点处两条曲线的切线互相垂直,求b和c的值.
(2)若a=c=1,b=0,试比较f(x)与g(x)的大小,并说明理由;
(3)若b=c=0,证明:对任意给定的正数a,总存在正数m,使得当x 时,恒有
时,恒有
f(x)>g(x)成立.
【原创】(本小题满分13分)已知数列{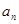 }中,
}中,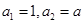 ,且
,且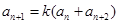 对任意正整数都成立,数列{
对任意正整数都成立,数列{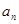 }的前n项和为Sn.
}的前n项和为Sn.
(1)若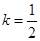 ,且
,且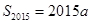 ,求a;
,求a;
(2)是否存在实数k,使数列{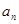 }是公比不为1的等比数列,且任意相邻三项
}是公比不为1的等比数列,且任意相邻三项 按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
(3)若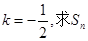 .
.