如图所示，粗糙的水平绝缘轨道与竖直放置的光滑绝缘的圆形轨道平滑连接，处于水平方向的匀强电场中，圆形轨道的最低点有A、B两带电小球，中间压缩一轻弹簧，弹簧与A、B均不连接，已知A、B两球的质量均为m，A、B两球均带正电，电量均为q，A球与水平轨道间的动摩擦因数为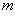
，
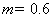，电场强度
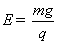，圆形轨道半径为R，由静止释放AB后，B恰能做完整的圆周运动。假定A、B球不再碰撞。求：从释放开始到A在水平轨道上运动的速度大小为其被释放时速度大小的一半时所需要的时间。（不计A、B间的静电作用，设弹簧弹力足够大，且作用时间极短）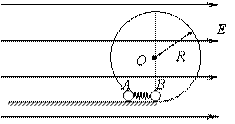
如图所示，一个光滑的圆锥体固定在水平圆盘上，其轴线沿竖直方向并与圆盘中心重合，母线与轴线之间的夹角为θ. 一条长为L的细绳，一端固定在圆锥体的顶点O处，另一端拴着一质量为m的小球（可视为质点）. 现让圆锥体绕其中心轴线由静止开始转动，求当其角速度由零增大到
且稳定时的过程中，细绳的拉力对小球所做的功.
如图所示，质量
的物体A与劲度k=500N/m的轻弹簧相连，弹簧的另一端与地面上的质量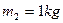
的物体B连接，A、B均处于静止状态. 当一质量
的物体C从A的正上方h=0.45m处自由下落，落到A上立刻与A粘连并一起向下运动，它们到达最低点后又向上运动，最终恰能使B离开地面但并不继续上升.（A、B、C均可视为质点，取g=10m/s2），求：
（1）C与A粘连后一起向下运动的速度；
（2）从AC一起运动直至最高点的过程中弹簧对AC整体做的功.
在倾角为θ的斜坡公路上，一质量m=10t的卡车从坡底开始上坡.经时间t=50s，卡车的速度从
=5m/s均匀增加到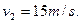
已知汽车在运动时受到的摩擦及空气阻力恒为车重的k倍（k=0.05），
，求：
（1）这段时间内汽车发动机的平均功率；
（2）汽车发动机在30s时的瞬时功率.
飞船完成了在顶定空间的科学技术试验后，返回舱开始按预定轨道从太空向地球表面返回. 返回舱开始时通过自身发动机进行调控以减速下降，进入大气层后，在一定的高度关闭发动机，打开阻力降落伞进一步减速下降. 这一过程中，返回舱所受空气摩擦阻力与其速度的平方成正比，比例系数（空气阻力系数）为k.若返回舱所受空气浮力忽略不计，且认为竖直降落，从阻力伞打开开始计时，返回舱运动的
图象如图中的AD曲线所示（其中CD段是平行横坐标轴的直线），已知返回舱的总质量为m，重力加速度g，求：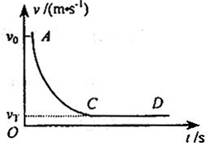
（1）空气阻力系数k的表达式；
（2）当返回舱的速度为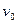
时，返回舱的加速度.
“蹦极”是一项近年流行的能使人获得强烈超重、失重感的非常刺激的惊险娱乐运动项目：人处在水面上方十层楼的高处，用弹性橡皮绳栓住脚踝，自高空自由下落，到一定位置时弹性绳拉紧，到接近水面时速度减为零，然后反弹. 已知某“勇敢者”头戴质量为1kg的安全帽从高处跳下，开始下落距水面的高度为76m，系统设计使人到落到离水面31m时弹性绳才绷直，此人静止下落至最低点的瞬间所用的时间是4s，求从弹性绳绷直到最低点的过程中，人的颈部对安全帽的平均作用力.（g=10m/s2）