已知椭圆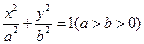 ,
,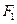 ,
,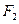 分别为其左、右焦点,
分别为其左、右焦点,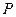 为椭圆上任意一点,
为椭圆上任意一点,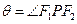 ,求
,求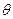 的最大值及
的最大值及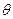 取得最大值时
取得最大值时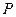 点的坐标.
点的坐标.
.选修4-1:几何证明选讲
已知C点在圆O直径BE的延长线上,CA切圆O于A点, DC是∠ACB的平分线交AE于点F,交AB于D点.
(1)求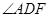 的度数.
的度数.
(2)若AB=AC,求AC:BC
已知函数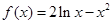 .
.
(I) 求函数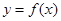 在
在 上的最大值.
上的最大值.
(II)如果函数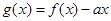 的图像与
的图像与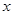 轴交于两点
轴交于两点 、
、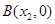 ,且
,且 .
. 是
是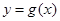 的导函数,若正常数
的导函数,若正常数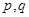 满足
满足 .
.
求证: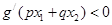 .
.
.若圆C过点M(0,1)且与直线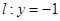 相切,设圆心C的轨迹为曲线E,A、B为曲线E上的两点,点
相切,设圆心C的轨迹为曲线E,A、B为曲线E上的两点,点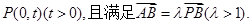
(I)求曲线E的方程;(II)若t=6,直线AB的斜率为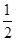 ,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;
,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;
(III)分别过A、B作曲线E的切线,两条切线交于点Q,若点Q恰好在直线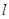 上,求证:t与
上,求证:t与 均为定值。
均为定值。
.某单位实行休年假制度三年以来,50名职工休年假的次数进行的调查统计结果
如下表所示:
根据上表信息解答以下问题:
(1)从该单位任选两名职工,用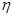 表示这两人休年假次数之和,记“函数
表示这两人休年假次数之和,记“函数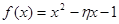 在区间
在区间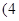 ,
,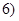 上有且只有一个零点”为事件
上有且只有一个零点”为事件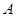 ,求事件
,求事件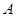 发生的概率
发生的概率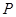 ;
;
(2)从该单位任选两名职工,用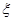 表示这两人休年假次数之差的绝对值,求随机变量
表示这两人休年假次数之差的绝对值,求随机变量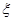 的分布列及数学期望
的分布列及数学期望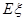 .
.
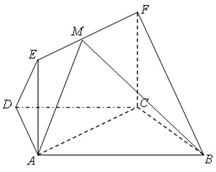
.如图,在梯形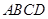 中,
中,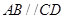 ,
,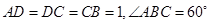 ,四边形
,四边形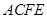 为矩形,平面
为矩形,平面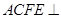 平面
平面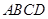 ,
,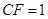 .
.
(I)求证: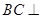 平面
平面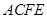 ;
;
(II)点 在线段
在线段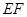 上运动,设平面
上运动,设平面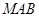 与平面
与平面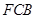 所成二面角的平面角为
所成二面角的平面角为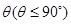 ,试求
,试求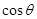 的取值范围.
的取值范围.