已知函数 ,恒过定点
,恒过定点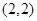 .
.
(1)求实数 ;
;
(2)在(1)的条件下,将函数 的图象向下平移1个单位,再向左平移
的图象向下平移1个单位,再向左平移 个单位后得到函数
个单位后得到函数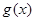 ,设函数
,设函数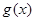 的反函数为
的反函数为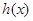 ,直接写出
,直接写出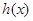 的解析式;
的解析式;
(3)对于定义在 上的函数
上的函数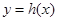 ,若在其定义域内,不等式
,若在其定义域内,不等式 恒成立,求实数
恒成立,求实数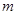 的取值范围.
的取值范围.
一种放射性元素,最初的质量为 ,按每年
,按每年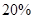 衰减.
衰减.
(1)求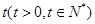 年后,这种放射性元素的质量
年后,这种放射性元素的质量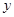 与
与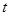 的函数关系式;
的函数关系式;
(2)求这种放射性元素的半衰期(质量变为原来的 时所经历的时间).(
时所经历的时间).(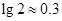 )
)
已知集合 ,集合
,集合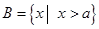 .
.
(1)若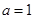 ,求
,求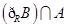 ;
;
(2)若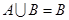 ,求
,求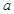 的取值范围.
的取值范围.
已知数列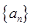 中,
中,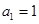 ,
, ,数列
,数列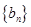 中,
中,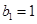 ,且点
,且点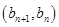 在直线
在直线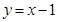 上.
上.
(Ⅰ)求数列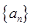 的通项公式;
的通项公式;
(Ⅱ)求数列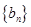 的通项公式;
的通项公式;
(Ⅲ)若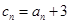 ,求数列
,求数列 的前项和
的前项和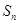 .
.
运货卡车以每小时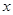 千米的速度匀速行驶130千米
千米的速度匀速行驶130千米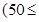
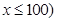 (单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油
(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.
(1)求这次行车总费用 关于
关于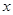 的表达式;
的表达式;
(2)当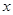 为何值时,这次行车的总费用最低,并求出最低费用的值.
为何值时,这次行车的总费用最低,并求出最低费用的值.