如图所示，宽L1m、倾角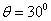的光滑平行导轨与电动势E3.0V、内-优题课

题文

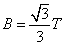如图所示，宽L=1m、倾角的光滑平行导轨与电动势E=3.0V、内阻r=0.5的电池相连接，处在磁感应强度、方向竖直向上的匀强磁场中。质量m=200g、电阻R=1的导体ab从静止开始运动。不计期于电阻，且导轨足够长。试计算：
（1）若在导体ab运动t=3s后将开关S合上，这时导体受到的安培力是多大？加速度是多少？
（2）导体ab的收尾速度是多大？
（3）当达到收尾速度时，导体ab的重力功率、安培力功率、电功率以及回路中焦耳热功率和化学功率各是多少？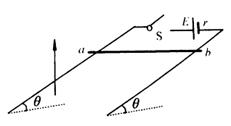

科目物理题型综合题难度中等

知识点：研究电磁感应现象

登录免费查看答案和解析

相关试题

如图所示，一根长 $L ＝ 1.5 m$ 的光滑绝缘细直杆 $M N$ ，竖直固定在场强为 $E ＝ 1.0 \times 10^{5} N / C$ 、与水平方向成 $θ ＝ 30 °$ 角的倾斜向上的匀强电场中。杆的下端 $M$ 固定一个带电小球 $A$ ，电荷量 $Q ＝ + 4.5 \times 10^{－ 6} C$ ；另一带电小球 $B$ 穿在杆上可自由滑动，电荷量 $q ＝ + 1.0 \times 10^{- 6} C$ ，质量 $m ＝ 1.0 \times 10^{- 2} k g$ 。现将小球 $B$ 从杆的上端 $N$ 静止释放，小球 $B$ 开始运动。（静电力常量 $k ＝ 9.0 \times 10^{9} N \cdot m^{2} ／ C^{2}$ ，取 $g ＝ 10 m / s^{2}$ ）

(1)小球 $B$ 开始运动时的加速度为多大？
(2)小球 $B$ 的速度最大时，距 $M$ 端的高度 $h_{1}$ 为多大？
(3)小球 $B$ 从 $N$ 端运动到距 $M$ 端的高度 $h_{2} ＝ 0.61 m$ 时，
速度为 $v = 1.0 m / s$ ，求此过程中小球 $B$ 的电势能改变了多少？

如图所示为研究电子枪中电子在电场中运动的简化模型示意图。在 $O x y$ 平面的 $A B C D$ 区域内，存在两个场强大小均为 $E$ 的匀强电场 $I$ 和 $I I$ ，两电场的边界均是边长为 $L$ 的正方形（不计电子所受重力）。

1.在该区域 $A B$ 边的中点处由静止释放电子，求电子离开 $A B C D$ 区域的位置。
2.在电场 $I$ 区域内适当位置由静止释放电子，电子恰能从 $A B C D$ 区域左下角 $D$ 处离开，求所有释放点的位置。
3.若将左侧电场 $I I$ 整体水平向右移动 $L / n (n \geq 1)$ 仍使电子从 $A B C D$ 区域左下角 $D$ 处离开（ $D$ 不随电场移动），求在电场 $I$ 区域内由静止释放电子的所有位置。 $x y = L^{2} (\frac{1}{2 n} + \frac{1}{4})$

带等量异种电荷的两平行金属板相距L，板长H，竖直放置，x轴从极板中点O通过，如图20所示。板间匀强电场的场强为E，且带正电的极板接地。将一质量为m、电量为+q的粒子（重力不计）从坐标为x₀处释放。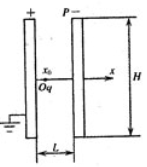

试从牛顿第二定律出发，证明该带电粒子在极板间运动的过程中，电势能与动能总和保持不变。
为使该粒子从负极板上方边缘的P点射出，须在x₀处使该粒子获得竖直向上的初速度v₀为多大?

如图6-16，金属杆ab的质量为m，长为L，通过的电流为I，处在磁感应强度为B的匀强磁场中，结果ab静止且紧压于水平导轨上.若磁场方向与导轨平面成θ角，求：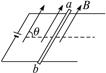

图6-16
(1)棒ab受到的摩擦力；
(2)棒ab对导轨的压力.

如图6-18所示，质量m＝1.0×10^-4 kg的小球放在绝缘的水平面上，小球带电荷量q＝2.0×10^-4 C，小球与水平面间的动摩擦因数μ＝0.2，外加水平向右的匀强电场E="5" V/m，垂直纸面向外的匀强磁场B＝2 T，小球从静止开始运动.
(1)小球具有最大加速度的值为多少？
(2)小球的最大速度为多少?(g取10 m/s²)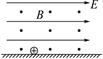

图6-18

试卷网试题网古诗词网作文网范文网