如图所示，两根水平平行固定的光滑金属导轨宽为L，足够长，在其上放里两根长也为L且与导轨垂直的金属棒ab和cd，它们的质量分别为2m、m，电阻阻值均为R（金属导轨及导线的电阻均可忽略不计），整个装置处在磁感应强度大小为B、方向竖直向下的匀强磁场中．
(1)现把金属棒ab锁定在导轨的左端，如图甲，对 cd施加与导轨平行的水平向右的恒力F，使金属棒cd向右沿导轨运动，当金属棒cd的运动状态稳定时，金属棒cd的运动速度是多大？
(2)若对金属棒ab解除锁定，如图乙，使金属棒cd获得瞬时水平向右的初速度v0，当它们的运动状态达到稳定的过程中，流过金属棒ab的电量是多少？整个过程中ab和cd相对运动的位移是多大？
如图7所示，一个光滑的弧形槽AB与水平粗糙轨道BC面相连接，另一圆形光滑轨道竖直放置与BC相切于C点，小球在离地面高h=0．45m的A点沿弧形槽静止开始滑下，进入水平轨道BC后，再进入圆形轨道内。已知小球在BC段动摩擦因数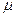
=0．25，BC长度为L=1m，圆形轨道半径为r=0．1m，g取l0m／s2，求：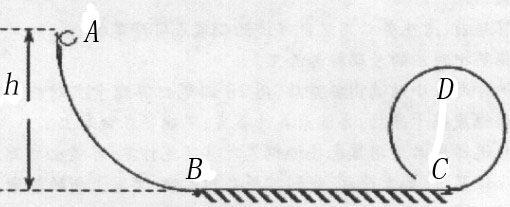
（1）小球滑到B点时和C点时的速度大小；
（2）要使小球能达到圆轨道的最高点D处，则小球在A速度至少为多少?
我国在2007年10月发射一颗绕月运行的探月卫星“嫦娥1号”。设“嫦娥1号”卫星环绕月球做圆周运动，在此圆轨道上运行周期为T。已知探月卫星轨道半径为R，引力常数为G。试求出：
（1）月球的质量；
（2）若月球表面的重力加速度为g，求月球的半径。
一个小球从距水平地面高80m，以30m／s的速度水平抛出，g取l0m／s2，忽略空气阻力。求：
（1）小球在空中运行的时间；
（2）小球落地时的速度大小；
（3）小球的水平射程。
皮球从某高度落到水平地板上，每弹跳一次上升的高度总等于前一次的0.64倍，且每次球与地面接触时间相等，空气阻力不计，与地面碰撞时，皮球重力可忽略。相邻两次球与地板碰撞的平均冲力大小之比是多少？
若用手拍这个球，保持在0.8m的高度上下跳动，则每次应给球施加的冲量大小为多少？已知球的质量m=0.5kg，g=10m/s2。
在水平面上有两个物体A和B，质量分别为mA=2kg，mB=1kg，A与B相距s=9.5m，A以υA=10m/s的初速度向静止的B运动，与B发生碰撞后分开仍沿原来方向运动。已知A从开始到碰后停止共运动了6s钟，问碰后B运动多少时间停止？（已知两物体与水平面间的动摩擦因数均为μ=0.1，g=10m/s2）