已知函数 .
.
(1)当函数 取得最大值时,求自变量
取得最大值时,求自变量 的集合;
的集合;
(2)该函数的图象可由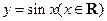 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到?
已知函数
(1)求 的最小正周期;(2)求
的最小正周期;(2)求 的单调区间;
的单调区间;
(3)求 图象的对称轴,对称中心.
图象的对称轴,对称中心.
若 ,求角
,求角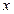 的取值范围.
的取值范围.
(本题满分13分) 如图所示,质点P在正方形ABCD的四个顶点上按逆时针方向前进.现在投掷一个质地均匀、每个面上标有一个数字的正方体玩具,它的六个面上分别写有两个1、两个2、两个3一共六个数字.质点P从A点出发,规则如下:当正方体上底面出现的数字是1,质点P前进一步(如由A到B);当正方体上底面出现的数字是2,质点P前进两步(如由A到C),
当正方体上底面出现的数字是3,质点P前进三步(如由A到 ).
).
在质点P转一圈之前连续投掷,若超过一圈,则投掷终止.
(Ⅰ)求点P恰好返回到A点的概率;
(Ⅱ)在点P转一圈恰能返回到A点的所有结果中,
用随机变量 表示点P恰能返回到A点的投掷次数,求
表示点P恰能返回到A点的投掷次数,求 的数学期望.
的数学期望.
(本题满分13分)已知函数f(x)= .(Ⅰ)求f(x)的定义域、值域;(Ⅱ)设α为锐角,且tan = ,求f(a)的值.
(本题满分13分)已知f(x)= 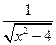 (x<-2),f(x)的反函数为g(x),点A(an,
(x<-2),f(x)的反函数为g(x),点A(an,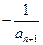 )在曲线y=g(x) (nÎN*)上,且a1=1。
)在曲线y=g(x) (nÎN*)上,且a1=1。
(Ⅰ)求y=g(x)的表达式;
(Ⅱ)证明数列{ }为等差数列。
}为等差数列。