(本题满分13分)已知f(x)= 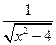 (x<-2),f(x)的反函数为g(x),点A(an,
(x<-2),f(x)的反函数为g(x),点A(an,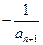 )在曲线y=g(x) (nÎN*)上,且a1=1。
)在曲线y=g(x) (nÎN*)上,且a1=1。
(Ⅰ)求y=g(x)的表达式;
(Ⅱ)证明数列{ }为等差数列。
}为等差数列。
已知向量 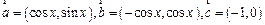 .
.
(1)若  ,求向量
,求向量  的夹角;
的夹角;
(2)已知  ,且
,且 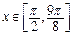 ,当
,当 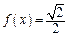 时,求 x的值并求
时,求 x的值并求 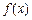 的值域.
的值域.
已知向量 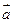 与
与 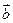 的夹角为60°,
的夹角为60°, 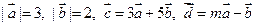 。
。
(1)求 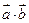 的值;(2)若
的值;(2)若  ,求实数
,求实数  的值。
的值。 
已知平面内两定点 ,动点
,动点 满足条件:
满足条件: ,设点
,设点 的轨迹是曲线
的轨迹是曲线 为坐标原点。
为坐标原点。
(I)求曲线 的方程;
的方程;
(II)若直线 与曲线
与曲线 相交于两不同点
相交于两不同点 ,求
,求 的取值范围;
的取值范围;
(III)(文科做)设 两点分别在直线
两点分别在直线 上,若
上,若 ,记
,记 分别为
分别为 两点的横坐标,求
两点的横坐标,求 的最小值。
的最小值。
(理科做)设 两点分别在直线
两点分别在直线 上,若
上,若 ,求
,求 面积的最大值。
面积的最大值。
设抛物线 的准线与
的准线与 轴交于点
轴交于点 ,焦点为
,焦点为 ;椭圆
;椭圆 以
以 为焦点,离心率
为焦点,离心率 。
。
(I)当 时,①求椭圆
时,①求椭圆 的标准方程;②若直线
的标准方程;②若直线 与抛物线交于
与抛物线交于 两点,且线段
两点,且线段 恰好被点
恰好被点 平分,设直线
平分,设直线 与椭圆
与椭圆 交于
交于 两点,求线段
两点,求线段 的长;
的长;
(II)(仅理科做)设抛物线 与椭圆
与椭圆 的一个交点为
的一个交点为 ,是否存在实数
,是否存在实数 ,使得
,使得 的边长是连续的自然数?若存在,求出这样的实数
的边长是连续的自然数?若存在,求出这样的实数 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
如图,已知平行六面体 。
。

(I)若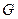 为
为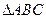 的重心,
的重心,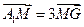 ,设
,设 ,用向量
,用向量 表示向量
表示向量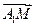 ;
;
(II)若平行六面体 各棱长相等且
各棱长相等且 平面
平面 ,
,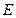 为
为 中点,
中点,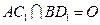 ,求证;
,求证;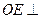 平面
平面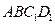 。
。