甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,甲先从6道备选题中一次性抽取3道题独立作答,然后由乙回答剩余3题,每人答对其中2题就停止答题,即闯关成功.已知在6道被选题中,甲能答对其中的4道题,乙答对每道题的概率都是.
(1)求甲、乙至少有一人闯关成功的概率;
(2)设甲答对题目的个数为ξ,求ξ的分布列.
(本小题满分14分)一片森林原面积为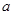 ,计划每年砍伐一些树,且每年砍伐面积的百分比相等,计划砍伐到面积一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的
,计划每年砍伐一些树,且每年砍伐面积的百分比相等,计划砍伐到面积一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的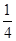 ,已知到今年为止,森林剩余面积为原的
,已知到今年为止,森林剩余面积为原的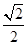 .
.
(1)求每年砍伐面积的百分比;
(2)到今年为止,该森林已砍伐了多少年;
(3)今后最多还能砍伐多少年?
(本小题满分13分)已知函数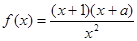 为偶函数.
为偶函数.
(1)求实数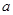 的值;
的值;
(2)记集合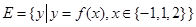 ,
,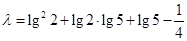 ,判断
,判断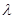 与
与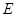 的关系;
的关系;
(3)当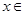
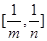
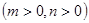 时,若函数
时,若函数 的值域为
的值域为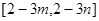 ,求
,求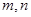 的值.
的值.
(本小题满分12分) 是定义在
是定义在 上的减函数,满足
上的减函数,满足 .
.
(1)求证: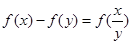 ;
;
(2)若 ,解不等式
,解不等式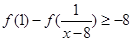 .
.
(本小题满分12分)已知函数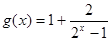 .
.
(1)用定义证明函数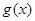 在
在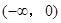 上为减函数.
上为减函数.
(2)求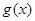 在
在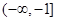 上的最小值.
上的最小值.
(本小题满分12分)已知方程 的两个不相等实根为
的两个不相等实根为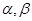 .集合
.集合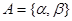 ,
, {2,4,5,6},
{2,4,5,6},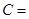 {1,2,3,4},A∩C=A,A∩B=
{1,2,3,4},A∩C=A,A∩B= ,求
,求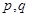 的值.
的值.