如图所示，质量M="3.5" kg的小车静止于光滑水平面上靠近桌子处，其上表面与水平桌面相平，小车长L="1.2" m，其左端放有一质量为m2="0.5" kg的滑块Q。水平放置的轻弹簧左端固定，质量为m1="1" kg的小物块P置于桌面上的A点并与弹簧的右端接触。此时弹簧处于原长，现用水平向左的推力将P缓慢推至B点(弹簧仍在弹性限度内)时，推力做的功为WF，撤去推力后，P沿桌面滑动到达C点时的速度为2 m/s，并与小车上的Q相碰，最后Q停在小车的右端，P停在距小车左端S="0.5" m处。已知AB间距L1="5" cm，A点离桌子边沿C点距离L2="90" cm，P与桌面间动摩擦因数μ1=0.4，P、Q与小车表面间动摩擦因数μ2=0.1。(g="10" m/s。)求：
(1)推力做的功WF；
(2)P与Q碰撞后瞬间Q的速度大小和小车最后速度v.
正电子发射计算机断层（PET）是分子水平上的人体功能显像的国际领先技术，它为临床诊断和治疗提供全新的手段。
（1）PET在心脏疾病诊疗中，需要使用放射正电子的同位素氮13示踪剂，氮13是由小型回旋加速器输出的高速质子轰击氧16获得的，反应中同时还产生另一个粒子，试写出该核反应方程。
（2）PET所用回旋加速器示意如图7.11，其中置于高真空中的金属D形盒的半径为R，两盒间距为d，在左侧D形盒圆心处放有粒子源S，匀强磁场的磁感应强度为B，方向如图所示。质子质量为m，电荷量为q。设质子从粒子源S进入加速电场时的初速度不计，质子在加速器中运动的总时间为t（其中已略去了质子在加速电场中的运动时间），质子在电场中的加速次数于回旋半周的次数相同，加速质子时的电压大小可视为不变。求此加速器所需的高频电源频率f和加速电压U。
（3）试推证当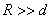
时，质子在电场中加速的总时间相对于在D形盒中回旋的时间可忽略不计（质子在电场中运动时，不考虑磁场的影响）。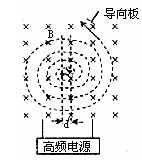
一如图所示，在倾角为θ的光滑斜面上端系一劲度系数为k的轻弹簧，弹簧下端连有一质量为m的小球，球被一垂直于斜面的挡板A挡住，此时弹簧没有形变。若手持挡板A以加速度a（a<gsinθ）沿斜面匀加速下滑，求：
（1）从挡板开始运动到球与挡板分离所经历的时间；
（2）从挡板开始运动到球速达到最大，球所经过的最小路程。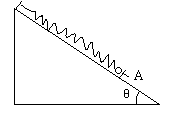
一位同学的家住在一座25层的高楼内，他每天乘电梯上楼，经过多次仔细观察和反复测量，他发现电梯启动后的运动速度符合如图所示的规律，他就根据这一特点在电梯内用台秤、重物和停表测量这座楼房的高度。他将台秤放在电梯内，将重物放在台秤的托盘，电梯从第一层开始启动，经过不间断地运行，最后停在最高层。在整个过程中，他记录了台秤在不同时间段内的示数，记录的数据如下表所示，但由于0~3.0s段的时间太短，他没有来得及将台秤的示数记录下来。假设在每个时间段内台秤的示数都是稳定的，重力加速度g取10m/s2。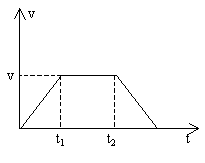
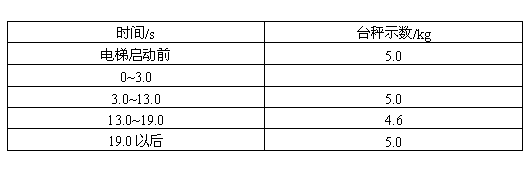
（1）电梯在0~3.0s内台秤的示数应该是多少？
（2）根据测量的数据，计算该座楼房每一层的平均高度。
一质点在一平面内运动，其轨迹如图所示。它从A点出发，以恒定速率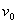
经时间t到B点，图中x轴上方的轨迹都是半径为R的半圆，下方的都是半径为r的半圆。
（1）求此质点由A到B沿x轴运动的平均速度。
（2）如果此质点带正电，且以上运动是在一恒定（不随时间而变）的磁场中发生的，试尽可能详细地论述此磁场的分布情况。不考虑重力的影响。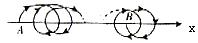
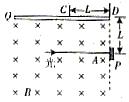
如图所示，一束波长为
的强光射在金属板P的A处发生了光电效应，能从A处向各个方向逸出不同速率的光电子。金属板P的左侧有垂直纸面向里的匀强磁场，磁感强度为B，面积足够大，在A点上方L处有一涂荧光材料的金属条Q，并与P垂直。现光束射到A处，金属条Q受到光电子的冲击而发出荧光的部分集中在CD间，且CD=L，光电子质量为m，电量为e，光速为c
（1）金属板P逸出光电子后带什么电？
（2）计算P板金属发生光电效应的逸出功W。
（3）从D点飞出的光电子中，在磁场中飞行的最短时间是多少？