(本小题满分13分)已知函数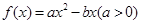 和
和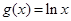 的图象有公共点P,且在点P处的切线相同.
的图象有公共点P,且在点P处的切线相同.
(Ⅰ)若点P的坐标为 ,求
,求 的值;
的值;
(Ⅱ)已知 ,求切点P的坐标.
,求切点P的坐标.
(本小题满分14分)如图,在四棱柱 中,
中,
 底面
底面 ,
,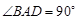 ,
, ,且
,且 ,点E在棱AB上,平面
,点E在棱AB上,平面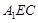 与棱
与棱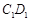 相交于点F.
相交于点F.
(Ⅰ)证明: ∥平面
∥平面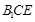 ;
;
(Ⅱ)若E是棱AB的中点,求二面角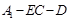 的余弦值;
的余弦值;
(Ⅲ)求三棱锥 的体积的最大值.
的体积的最大值.
(本小题满分13分)
现有两种投资方案,一年后投资盈亏的情况如下:
(1)投资股市:
| 投资结果 |
获利40% |
不赔不赚 |
亏损20% |
| 概率 |
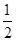 |
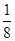 |
 |
(2)购买基金:
| 投资结果 |
获利20% |
不赔不赚 |
亏损10% |
| 概率 |
 |
 |
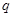 |
(Ⅰ)当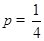 时,求q的值;
时,求q的值;
(Ⅱ)已知甲、乙两人分别选择了“投资股市”和“购买基金”进行投资,如果一年后他们中至少有一人获利的概率大于 ,求
,求 的取值范围;
的取值范围;
(Ⅲ)丙要将家中闲置的10万元钱进行投资,决定在“投资股市”和“购买基金”这两种方案中选择一种,已知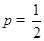 ,
, ,那么丙选择哪种投资方案,才能使得一年后投资收益的数学期望较大?给出结果并说明理由.
,那么丙选择哪种投资方案,才能使得一年后投资收益的数学期望较大?给出结果并说明理由.
(本小题满分13分)已知函数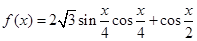 , x∈R的部分图象如图所示.
, x∈R的部分图象如图所示.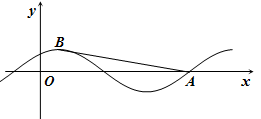
(Ⅰ)求函数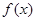 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(Ⅱ) 设点B是图象上的最高点,点A是图象与x轴的交点,求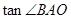 的值.
的值.
(本小题满分14分)已知动圆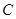 过定点
过定点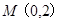 ,且在
,且在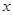 轴上截得弦长为
轴上截得弦长为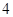 .设该动圆圆心的轨迹为曲线
.设该动圆圆心的轨迹为曲线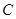 .
.
(1)求曲线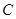 方程;
方程;
(2)点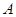 为直线
为直线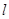 :
: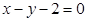 上任意一点,过
上任意一点,过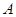 作曲线
作曲线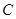 的切线,切点分别为
的切线,切点分别为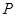 、
、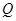 ,
,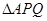 面积的最小值及此时点
面积的最小值及此时点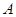 的坐标.
的坐标.