经过原点作圆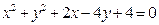 的割线,交圆于
的割线,交圆于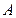 ,
,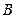 两点,求弦
两点,求弦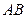 的中点
的中点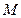 的轨迹方程.
的轨迹方程.
设函数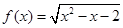 的定义域为集合
的定义域为集合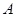 ,函数
,函数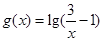 的定义域为集合
的定义域为集合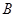 ,已知
,已知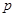 :
: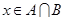 ;
;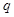 :
: 满足
满足 ,且若
,且若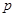 则
则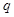 为真命题,求实数
为真命题,求实数 的取值范围.
的取值范围.
已知函数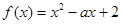 ,
, (
(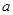 为常数)
为常数)
(1)当 时
时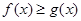 恒成立,求实数
恒成立,求实数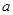 的取值范围;
的取值范围;
(2)若函数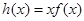 有对称中心为A(1,0),求证:函数
有对称中心为A(1,0),求证:函数 的切线
的切线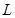 在切点处穿过
在切点处穿过 图象的充要条件是
图象的充要条件是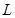 恰为函数在点A处的切线.(直线穿过曲线是指:直线与曲线有交点,且在交点左右附近曲线在直线异侧)
恰为函数在点A处的切线.(直线穿过曲线是指:直线与曲线有交点,且在交点左右附近曲线在直线异侧)
已知二次函数 与
与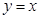 交于
交于 两点且
两点且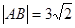 ,奇函数
,奇函数 ,当
,当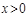 时,
时,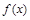 与
与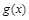 都在
都在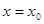 取到最小值.
取到最小值.
(1)求 的解析式;
的解析式;
(2)若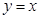 与
与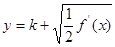 图象恰有两个不同的交点,求实数
图象恰有两个不同的交点,求实数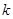 的取值范围.
的取值范围.
已知: 三个内角A,B,C所对的边,向量
三个内角A,B,C所对的边,向量 ,设
,设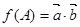
(1)若 ,求角
,求角 ;
;
(2)在(1)的条件下,若 ,求三角形ABC的面积.
,求三角形ABC的面积.
已知 是等差数列
是等差数列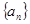 的前
的前 项和,满足
项和,满足 ;
; 是数列
是数列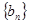 的前
的前 项和,满足:
项和,满足: .
.
(1)求数列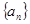 ,
,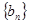 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 .
.