某沙漠地区经过治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的200个地块,从这些地块中用简单随机抽样的方法抽取20个作为样区,调查得到样本数据(xi,yi)(i=1,2,…,20),其中xi和yi分别表示第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得 , , , , .
(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);
(2)求样本(xi,yi)(i=1,2,…,20)的相关系数(精确到0.01);
(3)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野生动物数量更准确的估计,请给出一种你认为更合理的抽样方法,并说明理由.
附:相关系数r=
, ≈1.414.
≈1.414.
(本小题满分12分)已知 ,求下列各式的值
,求下列各式的值
⑴  ⑵
⑵
已知集合 是满足下列性质的函数
是满足下列性质的函数 的全体:在定义域
的全体:在定义域 内存在
内存在 ,使得
,使得
 成立.
成立.
(Ⅰ)函数 是否属于集合
是否属于集合 ? 说明理由;
? 说明理由;
(Ⅱ)若函数 属于集合
属于集合 ,试求实数
,试求实数 和
和 满足的约束条件;
满足的约束条件;
(Ⅲ)设函数 属于集合
属于集合 ,求实数
,求实数 的取值范围.
的取值范围.
已知二次函数 的图像过点
的图像过点 ,且有唯一的零点
,且有唯一的零点 .
.
(Ⅰ)求 的表达式;
的表达式;
(Ⅱ)当 时,求函数
时,求函数 的最小值
的最小值 .
.
医学上为研究某种传染病传播过程中病毒细胞的发展规律及其预防,将病毒细胞注入一只小白鼠体内进行实验,经检测,病毒细胞在体内的总数与天数的关系记录如下表.已知该种病毒细胞在小白鼠体内的个数超过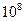 的时候小白鼠将死亡.但注射某种药物,将可杀死此时其体内该病毒细胞的
的时候小白鼠将死亡.但注射某种药物,将可杀死此时其体内该病毒细胞的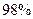 .
.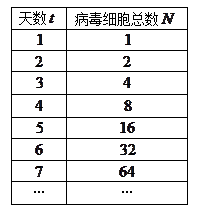
(Ⅰ) 为了使小白鼠在实验过程中不死亡,第一次最迟应在何时注射该种药物?(精确到天)
(Ⅱ)第二次最迟应在何时注射该种药物,才能维持小白鼠的生命?(精确到天)
(参考数据: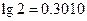 ,
, )
)
已知函数 .
.
(Ⅰ) 讨论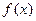 的奇偶性;
的奇偶性;
(Ⅱ)判断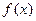 在
在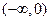 上的单调性并用定义证明.
上的单调性并用定义证明.