已知函数
.
(Ⅰ) 讨论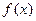
的奇偶性；
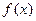（Ⅱ）判断在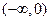
上的单调性并用定义证明.
在△ABC中,A最大,C最小,且A=2C,a+c=2b,求此三角形的三边之比.
已知方程tan2x一
tan x+1=0在x
[0，n
)( nN*)内所有根的和记为an
(1)写出an的表达式；(不要求严格的证明)
(2)记Sn = a1 + a2 +…+ an求Sn；
(3)设bn =(kn一5) ，若对任何nN* 都有an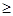
bn，求实数k的取值范围．
已知数列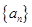
的前n项和
（n为正整数）。
（Ⅰ）令
，求证数列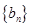
是等差数列，并求数列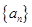的通项公式；
（Ⅱ）令
，
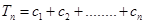试比较
与
的大小，并予以证明。
已知椭圆
的离心率为
，焦点到相应准线的距离为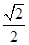
（1）求椭圆C的方程
（2）设直线与椭圆C交于A、B两点，坐标原点到直线的距离为
，求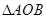
面积的最大值。
设数列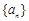
是有穷等差数列，给出下面数表：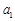
……
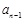
第1行
…… 
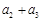第2行
… … …
… …
… 第n行
上表共有行，其中第1行的个数为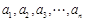
，从第二行起，每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数（按自上而下的顺序）分别为
．
（1）求证：数列成等比数列；
（2）若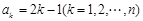
，求和
.