已知数列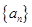
的前n项和
（n为正整数）。
（Ⅰ）令
，求证数列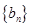
是等差数列，并求数列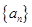的通项公式；
（Ⅱ）令
，
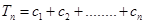试比较
与
的大小，并予以证明。
设命题
；命题
，使得
，如果命题
或
为真命题，命题且为假命题，求实数
的取值范围．
已知圆
：
，点
，
，点
在圆上运动，
的垂直平分线交
于点
．
（1）求动点的轨迹
的方程；
（2）设
分别是曲线上的两个不同点，且点
在第一象限，点
在第三象限，若
，
为坐标原点，求直线
的斜率
；
（3）过点
且斜率为
的动直线
交曲线于
两点，在
轴上是否存在定点
，使以
为直径的圆恒过这个点？若存在，求出的坐标，若不存在，说明理由．
已知椭圆
的方程为
，双曲线
的两条渐近线为
，
，过椭圆的右焦点
作直线
，使⊥，又l与交于
点，设与椭圆的两个交点由上至下依次为
．
（1）当与夹角为60°，双曲线的焦距为4时，求椭圆的方程及离心率；
（2）求
的最大值．
已知抛物线的顶点在原点，焦点在
轴正半轴上，抛物线上一点的横坐标为2，且该点到焦点的距离为2．
（1）求抛物线的标准方程；
（2）与圆
相切的直线
交抛物线于不同的两点
，若抛物线上一点
满足
，求
的取值范围。
已知“
，使等式
成立”是真命题．
（1）求实数
的取值集合
；
（2）设不等式
解集为
，若
是
的必要条件，求实数
的取值范围．