已知方程tan2x一 tan x+1=0在x
tan x+1=0在x [0,n
[0,n )( n
)( n N*)内所有根的和记为an
N*)内所有根的和记为an
(1)写出an的表达式;(不要求严格的证明)
(2)记Sn = a1 + a2 +…+ an求Sn;
(3)设bn =(kn一5)  ,若对任何n
,若对任何n N* 都有an
N* 都有an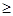 bn,求实数k的取值范围.
bn,求实数k的取值范围.
(本小题满分12分)
在数列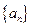 中,
中, ,
,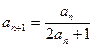
(I)求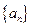 的通项公式。
的通项公式。
(II)若数列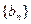 满足
满足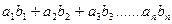 =
=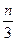 ,求数列
,求数列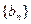 的通项公式
的通项公式
(本小题共12分)
已知△ABC顶点的直角坐标分别为A(3,4),B(0,0),C(c,0)
(1)若c=5,求sin∠A的值;
(2)若∠A是钝角,求c的取值范围。
已知椭圆C的中心在原点,焦点在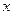 轴上,长轴长是短轴长的
轴上,长轴长是短轴长的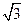 倍,其上一点到右焦点的最短距离为
倍,其上一点到右焦点的最短距离为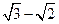 .
.
(1)求椭圆C的标准方程;
(2)若直线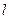 :
: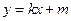 与圆O:
与圆O: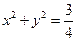 相切,且交椭圆C于A、B两点,
相切,且交椭圆C于A、B两点, 求当△AOB的面积最大时直线
求当△AOB的面积最大时直线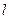 的方程.
的方程.
已知数列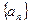 中
中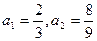 .当
.当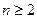 时
时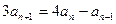 .(
.(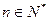 )
)
(Ⅰ)证明: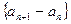 为等比数列;
为等比数列;
(Ⅱ) 求数列
求数列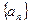 的通项;
的通项;
(Ⅲ)若数列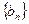 满足
满足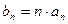 ,求
,求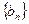 的前
的前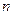 项和
项和 .
.
已知四棱锥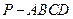 的三视图如下图所示,
的三视图如下图所示,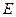 是侧棱
是侧棱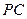 上的动点.
上的动点.
(1) 求四棱锥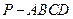 的体积;
的体积;
(2) 是否不论点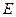 在何位置,都有
在何位置,都有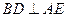 ?证明你的结论;
?证明你的结论;
(3) 若点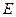 为
为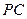 的中点,求二面角
的中点,求二面角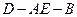 的大小.
的大小.