(本小题共12分)
已知△ABC顶点的直角坐标分别为A(3,4),B(0,0),C(c,0)
(1)若c=5,求sin∠A的值;
(2)若∠A是钝角,求c的取值范围。
某校有学生1200人,为了调查某种情况打算抽取一个样本容量为50的样本,问此样本若采用简单随机抽样将如何获得?
如果在一次试验中,某事件A发生的概率为p,那么在n次独立重复试验中,求事件A发生偶数次的概率.
某寻呼台共有客户3000人,若寻呼台准备了100份小礼品,邀请客户在指定时间来领取.假设任一客户去领奖的概率为4%.问:寻呼台能否向每一位顾客都发出奖邀请?若能使每一位领奖人都得到礼品,寻呼台至少应准备多少礼品?
某射手进行射击练习,每射击5发子弹算一组,一旦命中就停止射击,并进入下一组的练习,否则一直打完5发子弹后才能进入下一组练习,若该射手在某组练习中射击命中一次,并且已知他射击一次的命中率为0.8,求在这一组练习中耗用子弹数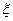 的分布列,并求出
的分布列,并求出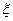 的期望
的期望 与方差
与方差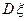 (保留两位小数).
(保留两位小数).
设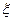 是一个离散型随机变量,其分布列如下表,求
是一个离散型随机变量,其分布列如下表,求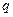 值,并求
值,并求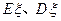 .
.
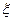 |
-1 |
0 |
1 |
| P |
 |
 |
 |