定义在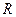 上的函
上的函 为常数)在x=-1处取得极值,且
为常数)在x=-1处取得极值,且 的图像在
的图像在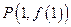 数处的切线平行与直线
数处的切线平行与直线 .
.
(1)求函数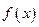 的解析式及极值;
的解析式及极值;
(2)设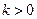 ,求不等式
,求不等式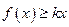 的解集;
的解集;
(3)对任意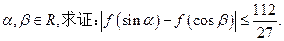
(满分12分)定义在R上的奇函数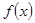 有最小正周期4,且
有最小正周期4,且 时,
时,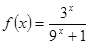 。
。
(1)求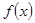 在
在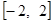 上的解析式;
上的解析式;
(2)判断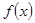 在(0,2)上的单调性,并给予证明;
在(0,2)上的单调性,并给予证明;
(3)当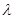 为何值时,关于方程
为何值时,关于方程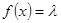 在
在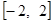 上有实数解?
上有实数解?
(满分12分)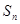 是等差数列
是等差数列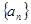 的前
的前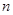 项和,
项和,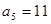 ,
,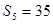 。
。
(1)求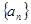 的通项公式;
的通项公式;
(2)设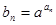 (
(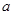 是实常数,且
是实常数,且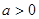 ),求
),求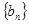 的前
的前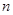 项和
项和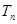 。
。
(满分12分)设命题P:关于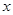 的不等式:
的不等式: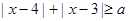 的解集是R,命题Q:函数
的解集是R,命题Q:函数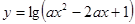 的定义域为R,若P或Q为真,P且Q为假,求
的定义域为R,若P或Q为真,P且Q为假,求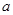 的取值范围。
的取值范围。
(满分10分)在△ABC中,角A,B,C所对的边分别为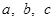 ,已知
,已知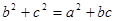 。
。
(1)求A的大小;
(2)如果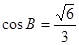 ,
,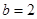 ,求△ABC的面积。
,求△ABC的面积。
已知函数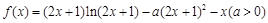 .
.
(1)若函数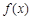 在
在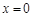 处取极值,求
处取极值,求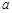 的值;
的值;
(2)如图,设直线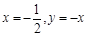 将坐标平面分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四个区域(不含边界),若函数
将坐标平面分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四个区域(不含边界),若函数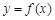 的图象恰好位于其中一个区域内,判断其所在的区域并求对应的
的图象恰好位于其中一个区域内,判断其所在的区域并求对应的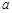 的取值范围;
的取值范围;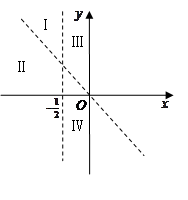
(3)比较 与
与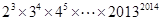 的大小,并说明理由.
的大小,并说明理由.