
(2009辽宁卷理)(本小题满分12分)
某人向一目射击4次,每次击中目标的概率为。该目标分为3个不同的部分,第一、二、三部分面积之比为1:3:6。击中目标时,击中任何一部分的概率与其面积成正比。
(Ⅰ)设X表示目标被击中的次数,求X的分布列;
(Ⅱ)若目标被击中2次,A表示事件“第一部分至少被击中1次或第二部分被击中2次”,求P(A) 

已知三个数 ,
, ,
,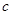 成等比数列,其公比为3,如果
成等比数列,其公比为3,如果 ,
,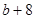 ,
, 成等差数列,求这三个数.
成等差数列,求这三个数.
(本题满分12分)已知三个集合
A={x|x2-3x+2=0},B={x|x2-ax+(a-1)=0},C={x|x2-bx+2=0},问同时满足B  A、C
A、C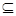 A的实数a、b是否存在?若存在,求出a、b所有值的集合;若不存在,请说明理由.
A的实数a、b是否存在?若存在,求出a、b所有值的集合;若不存在,请说明理由.
设集合P={4,3t+2,5t2},Q={3t-2,5t-6,5t2-1},且P∩Q={4},求实数t及P∪Q.
已知A={1,x,y},B={x,x2,xy}且A=B,求x、y;
(本小题满分10分)已知集合A={x|x2-3x+2=0},B={x|x2-ax+3a-5=0}.若A∩B=B,求实数a的取值范围.