(本小题满分13分)省环保研究所对市中心每天环境放射性污染情况进行调查研究后,发现一天中环境综合放射性污染指数 与时刻
与时刻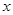 (时)的关系为
(时)的关系为 ,其中
,其中 是与气象有关的参数,且
是与气象有关的参数,且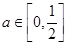 ,若用每天
,若用每天 的最大值为当天的综合放射性污染指数,并记作
的最大值为当天的综合放射性污染指数,并记作 .
.
(1)令 ,
, ,求t的取值范围;
,求t的取值范围;
(2)省政府规定,每天的综合放射性污染指数不得超过2,试问目前市中心的综合放射性污染指数是否超标?
已知函数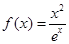 .
.
(Ⅰ)求函数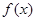 的单调区间;
的单调区间;
(Ⅱ)设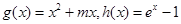 ,若在
,若在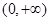 上至少存在一点
上至少存在一点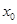 ,使得
,使得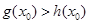 成立,求
成立,求 的范围.
的范围.
四棱锥P-ABCD中,PA⊥平面ABCD,E为AD的中点,ABCE为菱形,∠BAD=120°,PA=AB,G、F分别是线段CE、PB的中点.
(Ⅰ) 求证:FG∥平面PDC;
(Ⅱ) 求二面角 的正切值.
的正切值.
已知正项数列 的首项
的首项 ,前
,前 项和
项和 满足
满足 .
.
(Ⅰ)求证: 为等差数列,并求数列
为等差数列,并求数列 的通项公式;
的通项公式;
(Ⅱ)记数列 的前
的前 项和为
项和为 ,若对任意的
,若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知函数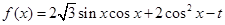 .
.
(Ⅰ)若方程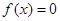 在
在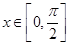 上有解,求
上有解,求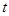 的取值范围;
的取值范围;
(Ⅱ)在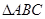 中,
中,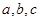 分别是A,B,C所对的边,若
分别是A,B,C所对的边,若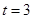 ,且
,且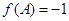 ,
,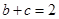 ,求
,求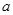 的最小值.
的最小值.
在极坐标系 中,直线
中,直线 的极坐标方程为
的极坐标方程为 是
是 上任意一点,点P在射线OM上,且满足
上任意一点,点P在射线OM上,且满足 ,记点P的轨迹为
,记点P的轨迹为 。
。
(Ⅰ)求曲线 的极坐标方程;
的极坐标方程;
(Ⅱ)求曲线 上的点到直线
上的点到直线 距离的最大值。
距离的最大值。