一质量为m、电荷量为q的小球,从O点以和水平方向成α角的初速度v0抛出,当达到最高点A时,恰进入一匀强电场中,如图,经过一段时间后,小球从A点沿水平直线运动到与A相距为S的A`点后又折返回到A点,紧接着沿原来斜上抛运动的轨迹逆方向运动又落回原抛出点,求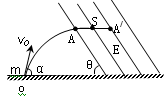
该匀强电场的场强E的大小和方向;(即求出图中的θ角,并在图中标明E的方向)
从O点抛出又落回O点所需的时间。
如图9-7所示,电源电动势ε=9V,内电阻r=0.5Ω,电阻R1=5.0Ω、R2=3.5Ω、R3=6.0Ω、R4=3.0Ω,电容C=2.0μF。当电键K由a与接触到与b接触通过R3的电量是多少?
如图所示电路,已知电源电动势ε=6.3V,内电阻r=0.5Ω,固定电阻R1=2Ω,R2=3Ω,R3是阻值为5Ω的滑动变阻器。按下电键K,调节滑动变阻器的触点,求通过电源的电流范围。
如图9-4所示,ε1=3V,r1=0.5Ω,R1=R2=5.5Ω,平行板电容器的两板距离d=1cm,当电键K接通时极板中的一个质量m=4×10-3g,电量为q=1.0×10-7C的带电微粒恰好处于静止状态。求:(1)K断开后,微粒向什么方向运动,加速度多大?(2)若电容为1000pF,K断开后,有多少电量的电荷流过R2?
在如图9-3所示电路中,R1=390Ω,R2=230Ω,电源内电阻r=50Ω,当K合在1时,电压表的读数为80V;当K合在2时,电压表的读数为U1=72V,电流表的读数为I1=0.18A,求:(1)电源的电动势(2)当K合在3时,两电表的读数。
如图10-2所示,AB为一光滑水平横杆,杆上套一质量为M的小圆环,环上系一长为L质量不计的细绳,绳的另一端拴一质量为m的小球,现将绳拉直,且与AB平行,由静止释放小球,则当线绳与AB成θ角时,圆环移动的距离是多少?