求下列极限:
如图,
和
所在平面互相垂直,且
,
,
分别为
的中点.
(1)求证:
平面
;
(2)求三棱锥
的体积.
附:椎体的体积公式
,其中
为底面面积,
为高.
某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
(1)根据表中数据,问是否有95%的把握认为"南方学生和北方学生在选用甜品的饮食习惯方面有差异";
(2)已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.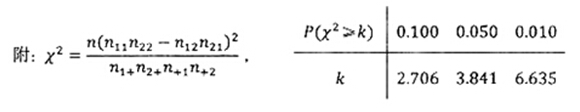
在
中,内角
的对边
,且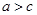 ,已知
,
,求:
,已知
,
,求:
(1)
和
的值;
(2)
的值.
已知函数
.
(1)求
的单调区间;
(2)记
为
的从小到大的第
个零点,证明:对一切
,有
.
如图5,
为坐标原点,双曲线
和椭圆
均过点
,且以
的两个顶点和
的两个焦点为顶点的四边形是面积为2的正方形.
(1)求
的方程;
(2)是否存在直线
,使得
与
交于
两点,与
只有一个公共点,且
?证明你的结论.