在直角坐标平面内,已知两点A(-2,0)及B(2,0),动点Q到点A的距离为6,线段BQ的垂直平分线交AQ于点P。
证明|PA|+|PB|为常数,并写出点P的轨迹T的方程;
在△ABC中,A、B、C所对的边分别是a、b、c,bcosB是acosC,ccosA的等差中项.
(1)求B的大小;
(2)若a+c= ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
已知数列是公差不为的等差数列,,且,,成等比数列.
(1)求数列的通项公式;
(2)设,求数列的前项和.
(本小题满分16分)已知函数 ,
, ,其中
,其中 为参数.
为参数.
(1)设 ,求
,求 的取值范围,并把
的取值范围,并把 表示为
表示为 的函数
的函数 ;
;
(2)求函数 的最大值(结果用
的最大值(结果用 表示);
表示);
(3)若对任意 ,都有
,都有 ,求实数
,求实数 的取值范围.(不需要过程,直接写出
的取值范围.(不需要过程,直接写出 的范围即可)
的范围即可)
(本小题满分16分)已知函数 ,(其中
,(其中 、
、 为参数)
为参数)
(1)当 时,证明:
时,证明: 不是奇函数;
不是奇函数;
(2)如果 是奇函数,求实数
是奇函数,求实数 、
、 的值;
的值;
(3)已知 ,在(2)的条件下,求不等式
,在(2)的条件下,求不等式 的解集.
的解集.
(本小题满分14分)已知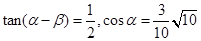 ,其中
,其中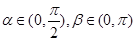 .
.
(1)求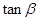 的值;
的值;
(2)求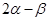 的值.
的值.