为调查某市老年人是否需要志愿者提供帮助,用简单随机抽样方法从该市调查了500位老年人,结果如右表.
| 性别 是否需要志愿者 |
男 |
女 |
| 需要 |
40 |
30 |
| 不需要 |
160 |
270 |
(1)估计该市老年人中, 需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该市的老年人是否需要志愿者提供帮助与性别有关?
附:
 (
( )
)
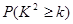 |
0.050 |
0.010 |
0.001 |
 |
3.841 |
6.635 |
10.828 |
已知函数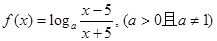 .
.
(1) 判断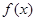 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(2) 设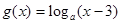 ,若方程
,若方程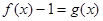 有实根,求
有实根,求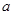 的取值范围;
的取值范围;
(3)是否存在实数m使得 为常数?若存在,求出m的值;若不存在,说明理由.
为常数?若存在,求出m的值;若不存在,说明理由.
已知定义在R上的函数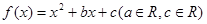 ,
,
定义: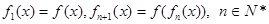 .
.
(1)若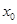 满足
满足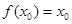 ,则称
,则称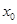 为函数
为函数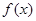 的不动点.若函数
的不动点.若函数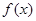 有两个不动点,求b,c满足的关系式;
有两个不动点,求b,c满足的关系式;
(2)若对任意的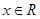 ,都使得
,都使得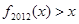 ,用反证法证明:
,用反证法证明: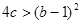 .
.
某产品生产厂家根据以往的生产销售经验得到下面有关销售的统计规律:每生产产品x(百台),其总成本为G(x)万元,其中固定成本为2万元,并且每生产100台的生产成本为1万元(总成本=固定成本+生产成本),销售收入R(x)(万元)满足R(x)=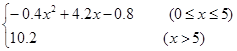 .假定该产品生产销售平衡,那么根据上述统计规律.
.假定该产品生产销售平衡,那么根据上述统计规律.
(1)要使工厂有盈利,产量x应控制在什么范围?
(2)工厂生产多少台产品时赢利最大?并求此时每台产品的售价为多少元?
已知集合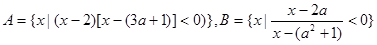 .
.
(1)当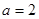 时,求
时,求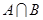 ;
;
(2)求使 的实数
的实数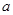 的取值范围.
的取值范围.
已知z为复数,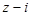 和
和 均为实数,其中
均为实数,其中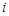 是虚数单位.
是虚数单位.
(1)求复数z;
(2)若复数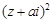 在复平面上对应的点在第一象限,求实数a的取值范围.
在复平面上对应的点在第一象限,求实数a的取值范围.