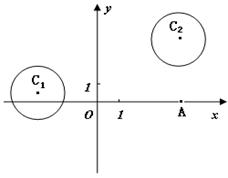
在平面直角坐标系
中,已知圆
和圆
.
(1)若直线
过点
,且被圆
截得的弦长为
,求直线
的方程;
(2)设 为平面上的点,满足:存在过点 的无穷多对互相垂直的直线 和 ,它们分别与圆 和圆 相交,且直线 被圆 截得的弦长与直线 被圆 截得的弦长相等,试求所有满足条件的点P的坐标.
(本小题满分13分)已知经过抛物线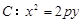 焦点
焦点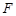 的直线
的直线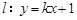 与抛物线
与抛物线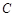 交于
交于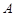 、
、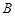 两点,若存在一定点
两点,若存在一定点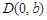 ,使得无论
,使得无论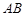 怎样运动,总有直线
怎样运动,总有直线 的斜率与
的斜率与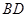 的斜率互为相反数.
的斜率互为相反数.
(1)求 与
与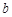 的值;
的值;
(2)对于椭圆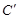 :
: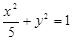 ,经过它左焦点
,经过它左焦点 的直线
的直线 与椭圆
与椭圆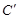 交于
交于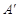 、
、 两点,是否存在定点
两点,是否存在定点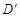 ,使得无论
,使得无论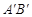 怎样运动,都有
怎样运动,都有 ?若存在,求出
?若存在,求出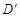 坐标;若不存在,说明理由.
坐标;若不存在,说明理由.
(本小题满分13分)如图,在正三棱柱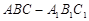 中,已知
中,已知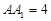 ,
,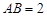 ,
,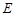 是
是 的中点,
的中点,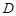 在棱
在棱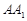 上.
上.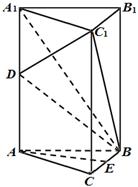
(1)求异面直线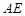 与
与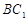 所成角;
所成角;
(2)若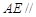 平面
平面 ,求
,求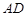 长;
长;
(3)在棱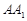 上是否存在点
上是否存在点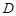 ,使得二面角
,使得二面角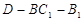 的大小等于
的大小等于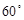 ,若存在,求
,若存在,求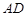 的长;若不存在,说明理由.
的长;若不存在,说明理由.
(本小题满分13分)椭圆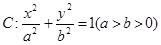 的左、右焦点分别是
的左、右焦点分别是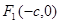 ,
,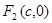 ,过
,过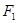 斜率为1的直线与椭圆
斜率为1的直线与椭圆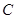 相交于
相交于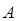 ,
,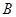 两点,且
两点,且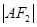 ,
,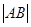 ,
,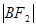 成等差数列.
成等差数列.
(1)请探求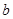 与
与 的关系;
的关系;
(2)设点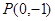 在线段
在线段 的垂直平分线上,求椭圆
的垂直平分线上,求椭圆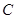 的方程.
的方程.
(本小题满分12分)如图所示,直三棱柱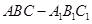 中,
中,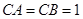 ,
, ,棱
,棱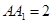 ,
, 分别是
分别是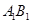 、
、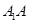 的中点.
的中点.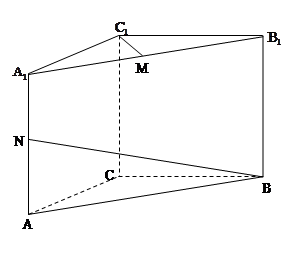
(1)求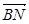 的长;
的长;
(2)求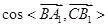 的值;
的值;
(3)求证: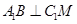 .
.
(本小题满分12分) 已知命题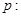
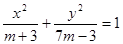 表示焦点在
表示焦点在 轴的双曲线,命题
轴的双曲线,命题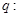
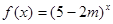 是增函数,若
是增函数,若 或
或 为真命题,
为真命题, 且
且 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.