(本小题满分12分)
某市统计局就某地居民的月收入调查了 10 000 人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1 000,1500)).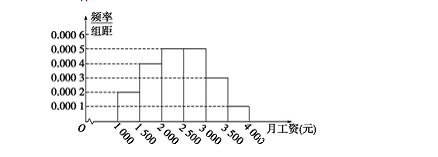
(1)求居民收入在[3 000,3 500)的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这 10 000 人中按分层抽样方法抽出 100 人作进一步分析,则月收入在[2 500,3 000)的这段应抽取多少人?
【原创】(本小题满分14分)已知数列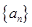 与
与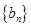 满足
满足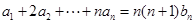 ,
,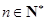 .
.
(Ⅰ)若
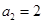 ,求
,求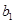 ,
,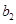 ;
;
(Ⅱ)若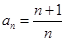 ,求证:
,求证: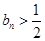 ;
;
(Ⅲ)若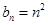 ,求数列
,求数列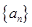 的通项公式.
的通项公式.
【原创】(本小题满分12分)如图,在三棱锥 中,
中, 底面ABC,
底面ABC, ,AP=AC, 点
,AP=AC, 点 ,
, 分别在棱
分别在棱 上,且BC//平面ADE.
上,且BC//平面ADE.
(Ⅰ)求证:DE⊥平面 ;
;
(Ⅱ)若PC⊥AD,且三棱锥 的体积为8,求多面体ABCED的体积.
的体积为8,求多面体ABCED的体积.
【改编】(本小题满分12分)已知某校 四个社团的学生人数分别为10,5,20,15.现为了了解社团活动开展情况,用分层抽样的方法从
四个社团的学生人数分别为10,5,20,15.现为了了解社团活动开展情况,用分层抽样的方法从 四个社团的学生当中随机抽取10名学生参加问卷调查.
四个社团的学生当中随机抽取10名学生参加问卷调查.
(Ⅰ)从 四个社团中各抽取多少人?
四个社团中各抽取多少人?
(Ⅱ)在社团 所抽取的学生总数中,任取2个,求
所抽取的学生总数中,任取2个,求 社团中各有1名学生的概率.
社团中各有1名学生的概率.
【原创】(本小题满分12分)已知函数 .
.
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)求 在
在 上的最大值与最小值.
上的最大值与最小值.
(本小题满分12分)设 到定点
到定点 的距离和它到直线
的距离和它到直线 距离的比是
距离的比是 .
.
(Ⅰ)求点 的轨迹方程;
的轨迹方程;
(Ⅱ) 为坐标原点,斜率为
为坐标原点,斜率为 的直线过
的直线过 点,且与点
点,且与点 的轨迹交于点
的轨迹交于点 ,
, ,若
,若 ,求△
,求△ 的面积.
的面积.