求解不等式 。
。
(本小题满分13分)时下,网校教学越越受到广大学生的喜爱,它已经成为学生们课外学习的一种趋势,假设某网校的套题每日的销售量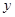 (单位:千套)与销售价格
(单位:千套)与销售价格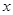 (单位:元/套)满足的关系式
(单位:元/套)满足的关系式 ,其中
,其中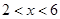 ,
,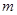 为常数.已知销售价格为4元/套时,每日可售出套题21千套.
为常数.已知销售价格为4元/套时,每日可售出套题21千套.
(1)求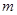 的值;
的值;
(2)假设网校的员工工资、办公等所有开销折合为每套题2元(只考虑销售出的套数),试确定销售价格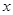 的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
(本小题满分13分)在等差数列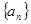 中,
中, ,其前
,其前 项和为
项和为 ,等比数列
,等比数列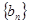 的各项均为正数,
的各项均为正数, ,公比为
,公比为 ,且
,且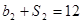 ,
,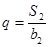 .
.
(1)求 与
与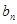 ;
;
(2)设数列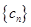 满足
满足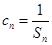 ,求
,求 的前
的前 项和
项和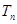 .
.
(本小题满分13分) 已知函数
(1)当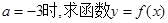 的极值点;
的极值点;
(2)当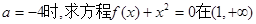 上的根的个数.
上的根的个数.
(本小题满分12分)已知中心在原点的椭圆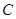 的离心率
的离心率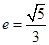 ,一条准线方程为
,一条准线方程为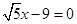
(1)求椭圆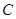 的标准方程;
的标准方程;
(2)若以 >0)为斜率的直线
>0)为斜率的直线 与椭圆
与椭圆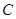 相交于两个不同的点
相交于两个不同的点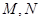 ,且线段
,且线段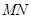 的垂直平分线与两坐标轴围成的三角形的面积为
的垂直平分线与两坐标轴围成的三角形的面积为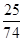 ,求
,求 的取值范围。
的取值范围。
(本小题满分12分)某商店商品每件成本10元,若售价为25元,则每天能卖出288件,经调查,如果降低价格,销售量可以增加,且每天多卖出的商品件数t与商品单价的降低值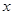 (单位:元,
(单位:元,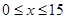 )的关系是t=
)的关系是t= .
.
(1)将每天的商品销售利润y表示成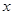 的函数;
的函数;
(2)如何定价才能使每天的商品销售利润最大?