(本小题满分13分)时下,网校教学越越受到广大学生的喜爱,它已经成为学生们课外学习的一种趋势,假设某网校的套题每日的销售量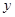 (单位:千套)与销售价格
(单位:千套)与销售价格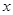 (单位:元/套)满足的关系式
(单位:元/套)满足的关系式 ,其中
,其中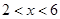 ,
,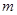 为常数.已知销售价格为4元/套时,每日可售出套题21千套.
为常数.已知销售价格为4元/套时,每日可售出套题21千套.
(1)求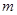 的值;
的值;
(2)假设网校的员工工资、办公等所有开销折合为每套题2元(只考虑销售出的套数),试确定销售价格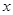 的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
(本小题满分 分)
分)
已知函数 ,
,
(1)判断函数的奇偶性;
(2)求函数 的值域。
的值域。
本小题满分10分)
已知集合A={x|ax2-3x+2=0,a∈R},若A中至多只有一个元素,求a的取值范围
已知函数 .
.
(1)求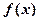 在
在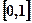 上的最大值;
上的最大值;
(2)若对任意的实数 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)若关于 的方程
的方程 在
在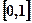 上恰有两个不同的实根,求实数
上恰有两个不同的实根,求实数 的取值范围.
的取值范围.
已知圆 及定点
及定点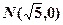 ,点
,点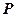 是圆
是圆 上的动点,
上的动点,
点 在
在 上,点
上,点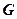 在
在 上,且满足
上,且满足 ,
, .
.
(1)求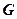 的轨迹
的轨迹 的方程;
的方程;
(2)过点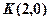 作直线
作直线 ,与曲线
,与曲线 交于
交于 两点,
两点, 为坐标原点,设
为坐标原点,设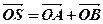 ,是否存在这样的直线
,是否存在这样的直线 ,使四边形
,使四边形 的对角线相等?若存在,求出直线
的对角线相等?若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
已知直线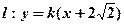 与圆
与圆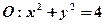 相交于
相交于 两点,
两点,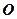 为坐标原点,
为坐标原点, 的面积为
的面积为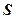 .
.
(1)试将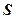 表示成
表示成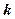 的函数
的函数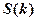 ,并求出其定义域;
,并求出其定义域;
(2)求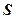 的最大值,并求取得最大时
的最大值,并求取得最大时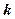 的值.
的值.