(本小题满分〗2分)
在三棱锥S -ABC中,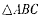 是边长为4的正三角形,点S在平面ABC上的射影恰为AC的中点,
是边长为4的正三角形,点S在平面ABC上的射影恰为AC的中点,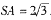 ,M、N分别为AB、SB的中点.
,M、N分别为AB、SB的中点.
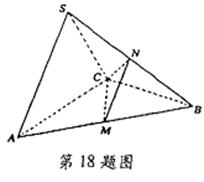
(1) 证明AC丄SB;
(2) 求直线CN与平面ABC所成角的余弦值;
(3) 求点B到平面CMN的距离
在图一所示的平面图形中, 是边长为
是边长为  的等边三角形,
的等边三角形,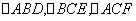 是分别以
是分别以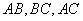 为底的全等的等腰三角形,现将该平面图形分别沿
为底的全等的等腰三角形,现将该平面图形分别沿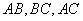 折叠,使
折叠,使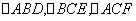 所在平面都与平面
所在平面都与平面 垂直,连接
垂直,连接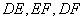 ,得到图二所示的几何体,据此几何体解决下面问题.
,得到图二所示的几何体,据此几何体解决下面问题.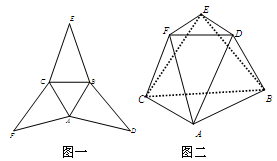
(1)求证: ;
;
(2)当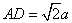 时,求三棱锥
时,求三棱锥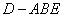 的体积
的体积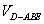 ;
;
(3)在(2)的前提下,求二面角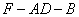 的余弦值.
的余弦值.
不等式选讲
设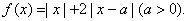
(1)当a=l时,解不等式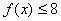 ;
;
(2)若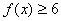 恒成立,求正实数a的取值范围。
恒成立,求正实数a的取值范围。
坐标系与参数方程
已知圆锥曲线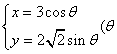 为参数)和定点
为参数)和定点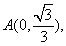 F1,F2是圆锥曲线的左右焦点。
F1,F2是圆锥曲线的左右焦点。
(1)求经过点F2且垂直于直线AF1的直线l的参数方程;
(2)以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,求直线AF2的极坐标方程。
如图,已知圆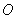 外有一点
外有一点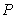 ,作圆
,作圆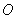 的切线
的切线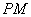 ,
,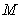 为切点,过
为切点,过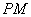 的中点
的中点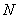 ,作割线
,作割线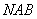 ,交圆于
,交圆于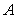 、
、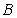 两点,连接
两点,连接 并延长,交圆
并延长,交圆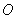 于点
于点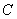 ,连续
,连续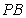 交圆
交圆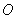 于点
于点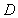 ,若
,若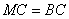 .
.
(1)求证:△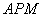 ∽△
∽△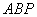 ;
;
(2)求证:四边形 是平行四边形.
是平行四边形.
已知函数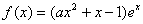 ,其中
,其中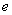 是自然对数的底数,
是自然对数的底数, .
.
(1)若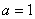 ,求曲线
,求曲线 在点
在点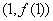 处的切线方程;
处的切线方程;
(2)若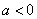 ,求
,求 的单调区间;
的单调区间;
(3)若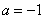 ,函数
,函数 的图象与函数
的图象与函数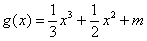 的图象有3个不同的交点,求实数
的图象有3个不同的交点,求实数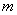 的取值范围.
的取值范围.