(本题满分12)
定义在R上的函数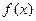 满足
满足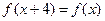 ,当2≤x≤6时,
,当2≤x≤6时,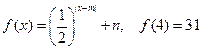 。
。
(1)求m ,n的值;
(2)比较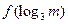 与
与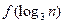 的大小
的大小
在△ABC中,已知 ,
,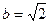 ,B=45°求A、C及c (结论保留最简根式形式)
,B=45°求A、C及c (结论保留最简根式形式)
(本小题满分14分)已知函数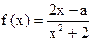 (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数.
(Ⅰ)求实数a的值所组成 的集合A;
的集合A;
(Ⅱ)设关于x的方程 的两实数根为x1、x2,试问:是否存在实数m,使得不等式
的两实数根为x1、x2,试问:是否存在实数m,使得不等式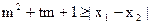 对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由?
对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由?
(本小题满分14分)已知两点M(-1,0), N(1,  0), 且点P使
0), 且点P使 成公差小于零的等差数列.
成公差小于零的等差数列.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)若点P的坐标为(x0, y0), 记θ为 ,
, 的夹角, 求
的夹角, 求
(本小题满分13分)某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口的O北偏西30°且与该港口相距20海里的A处,并正以30海里 /小时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向
/小时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向 以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇
以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇 .
.
(I)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(II)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值.
(本小题满分13分)若 =
= ,
, =
= ,其中
,其中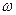 >0,记函数f(x)=(
>0,记函数f(x)=( +
+ )·
)· +k.
+k.
(1)若f(x)图象中相邻两条对称轴间的距离不小于 ,求
,求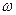 的取值范围.
的取值范围.
(2)若f(x)的最小正周期为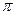 ,且当x
,且当x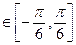 时,f(x)的最大值是
时,f(x)的最大值是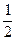 ,求f(x)的解析式,
,求f(x)的解析式,