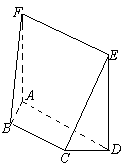
如图,在五面体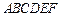 中,四边形
中,四边形 是正方形,
是正方形,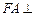 平面
平面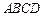 ,
, ∥
∥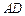 ,
,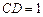 ,
, 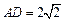 ,
, 。
。
(Ⅰ)求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(Ⅱ)证明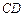 ⊥平面
⊥平面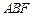 ;
;
(Ⅲ)求二面角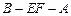 的正切值
的正切值
某种有奖销售的饮料,瓶盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为 .甲、乙、丙三位同学每人购买了一瓶该饮料。
.甲、乙、丙三位同学每人购买了一瓶该饮料。
(1)求甲中奖且乙、丙都没有中奖的概率;
(2)求中奖人数ξ的分布列及数学期望Eξ
已知函数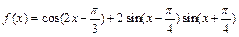
(1)求函数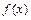 的最小正周期和图象的对称轴方程
的最小正周期和图象的对称轴方程
(2)求函数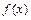 在区间
在区间 上的值域
上的值域
已知点 和互不相同的点
和互不相同的点 ,
,
满足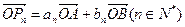 ,其中
,其中 分别为等差数列和等比数列,O为坐标原点,若
分别为等差数列和等比数列,O为坐标原点,若 为线段AB的中点。
为线段AB的中点。
(1)求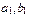 的值;
的值;
(2)证明 的公差为d =0,或
的公差为d =0,或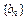 的公比为q=1,点
的公比为q=1,点 在同一直线上;
在同一直线上;
(3)若d  0,且q
0,且q  1,点
1,点 能否在同一直线上?证明你的结论
能否在同一直线上?证明你的结论
设实 数
数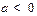 , 设函数
, 设函数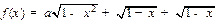 的最大值为
的最大值为 。
。
(1)设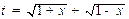 ,求
,求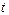 的取值范围,并把
的取值范围,并把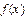 表示为
表示为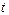 的函数
的函数 ;
;
(2)求