某种有奖销售的饮料,瓶盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为 .甲、乙、丙三位同学每人购买了一瓶该饮料。
.甲、乙、丙三位同学每人购买了一瓶该饮料。
(1)求甲中奖且乙、丙都没有中奖的概率;
(2)求中奖人数ξ的分布列及数学期望Eξ
已知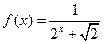 ,分别求
,分别求 ,
,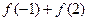 ,
,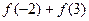 ,然后归纳猜想一般性结论,并证明你的结论.
,然后归纳猜想一般性结论,并证明你的结论.
已知非零实数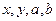 ,
,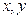 分别为
分别为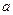 与
与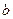 ,
,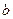 与
与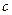 的等差中项,`且满足
的等差中项,`且满足 ,求证:非零实数
,求证:非零实数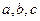 成等比数列.
成等比数列.
已知实数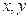 满足:
满足: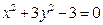 ,求
,求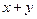 的取值范围.
的取值范围.
(本小题共13分)
用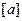 表示不大于
表示不大于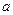 的最大整数.令集合
的最大整数.令集合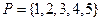 ,对任意
,对任意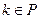 和
和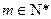 ,定义
,定义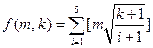 ,集合
,集合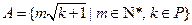 ,并将集合
,并将集合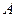 中的元素按照从小到大的顺序排列,记为数列
中的元素按照从小到大的顺序排列,记为数列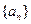 .
.
(Ⅰ)求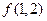 的值;
的值;
(Ⅱ)求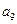 的值;
的值;
(Ⅲ)求证:在数列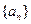 中,不大于
中,不大于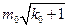 的项共有
的项共有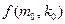 项.
项.
(本小题共14分)
已知抛物线P:x2="2py" (p>0).
(Ⅰ)若抛物线上点 到焦点F的距离为
到焦点F的距离为 .
.
(ⅰ)求抛物线 的方程;
的方程;
(ⅱ)设抛物线 的准线与y轴的交点为E,过E作抛物线
的准线与y轴的交点为E,过E作抛物线 的切线,求此切线方程;
的切线,求此切线方程;
(Ⅱ)设过焦点F的动直线l交抛物线于A,B两点,连接 ,
, 并延长分别交抛物线的准线于C,D两点,求证:以CD为直径的圆过焦点F.
并延长分别交抛物线的准线于C,D两点,求证:以CD为直径的圆过焦点F.