已知 ,
,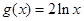 ,
,
(1)若对 内的一切实数
内的一切实数 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(2)当 时,求最大的正整数
时,求最大的正整数 ,使得对
,使得对 (
( 是自然对数的底数)内的任意
是自然对数的底数)内的任意 个实数
个实数 都有
都有 成立;
成立;
(3)求证: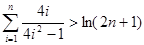
 .
.
已知椭圆 的中心在坐标原点,两个焦点分别为
的中心在坐标原点,两个焦点分别为 ,
,
 ,点
,点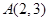 在椭圆
在椭圆 上,过点
上,过点 的直线
的直线 与抛物线
与抛物线 交于
交于 两点,抛物线
两点,抛物线 在点
在点 处的切线分别为
处的切线分别为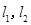 ,且
,且 与
与 交于点
交于点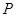 .
.
(1) 求椭圆 的方程;
的方程;
(2) 是否存在满足 的点
的点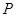 ? 若存在,指出这样的点
? 若存在,指出这样的点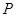 有几个(不必求出点
有几个(不必求出点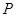 的坐标); 若不存在,说明理由.
的坐标); 若不存在,说明理由.
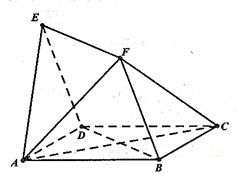
如图,四边形 与
与 均为菱形,
均为菱形, ,且
,且 .
.
(1)求证: ;
;
(2)求证: ;
;
(3)求二面角 的余弦值.
的余弦值.
某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为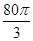 立方米,且
立方米,且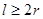 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为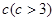 千元,设该容器的建造费用为
千元,设该容器的建造费用为 千元.
千元.
(1)写出 关于
关于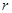 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(2)求该容器的建造费用最小时的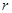 .
.
数列 的前
的前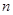 项和为
项和为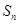 ,且
,且
(1)写出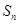 与
与 的递推关系式
的递推关系式 ,并求
,并求 ,
, ,
, 的值;
的值;
(2)猜想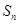 关于
关于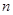 的表达式,并用数学归纳法证明.
的表达式,并用数学归纳法证明.