(本小题满分13分)
设数列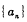 的前n项和为
的前n项和为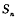 ,对一切
,对一切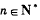 ,点(
,点(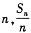 )都在函数
)都在函数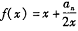 的图象上.
的图象上.
(1) 求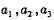 的值,猜想
的值,猜想 的表达式,并证明你的猜想;
的表达式,并证明你的猜想;
(2) 设
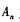 为数列
为数列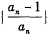 的前项积,是否存在实数、使得不等式
的前项积,是否存在实数、使得不等式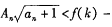
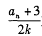 对一切
对一切 都成立?若存在,求出k的取值范围,若不存在,说明理由.
都成立?若存在,求出k的取值范围,若不存在,说明理由.
(13分)已知函数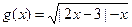 的定义域为集合
的定义域为集合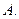
(1)求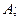
(2)若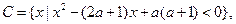
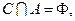 求实数
求实数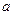 的取值范围.
的取值范围.
2006年8月中旬,湖南省资兴市遇到了百年不遇的洪水灾害。在资兴市的东江湖岸边的O点处(可视湖岸为直线)停放着一只救人的小船,由于缆绳突然断开,小船被风刮跑,其方向与湖岸成15°,速度为2.5km/h,同时岸上一人,从同一地点开始追赶小船,已知他在岸上追的速度为4 km/h,在水中游的速度为2 km/h,问此人能否追上小船?若小船速度改变,则小船能被此人追上的最大速度是多少
如图表示 电流 I 与时间t的函数关系式: I =
电流 I 与时间t的函数关系式: I =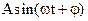 在同一周期内的图象。
在同一周期内的图象。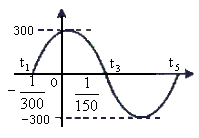
(1)根据图象写出I 的解析式;
(2)为了使I =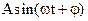 中t在任意-段
中t在任意-段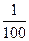 秒的时间内电流I能同时取得最大值和最小值,那么正整数
秒的时间内电流I能同时取得最大值和最小值,那么正整数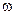 的最小值是多少?
的最小值是多少?
已知函数f(x)=4sin2(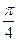 +x)-2
+x)-2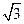 cos2x-1(x∈R)
cos2x-1(x∈R)
(1)求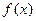 的最小正周期、最大值及最小值;
的最小正周期、最大值及最小值;
(2)求f(x)的图象的对称轴方程
已知复数z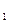 满足:(1)
满足:(1)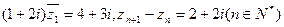 .
.
(1)求复数z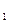 (2)求满足
(2)求满足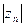
 的最大正整数n.
的最大正整数n.