如图表示 电流 I 与时间t的函数关系式: I =
电流 I 与时间t的函数关系式: I =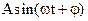 在同一周期内的图象。
在同一周期内的图象。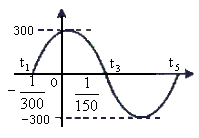
(1)根据图象写出I 的解析式;
(2)为了使I =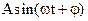 中t在任意-段
中t在任意-段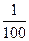 秒的时间内电流I能同时取得最大值和最小值,那么正整数
秒的时间内电流I能同时取得最大值和最小值,那么正整数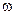 的最小值是多少?
的最小值是多少?
 的内角
的内角 满足
满足 (单位向量
(单位向量 互相垂直),且
互相垂直),且 .
.
(1)求 的值;
的值;
(2)若 ,边长
,边长 ,求边长
,求边长 .
.
如图,三棱锥 中,侧面
中,侧面 是等边三角形,
是等边三角形, 是
是 的中心.
的中心.
(1)若 ,求证
,求证 ;
;
(2)若 上存在点
上存在点 ,使
,使 平面
平面 ,求
,求 的值.
的值.
已知 函数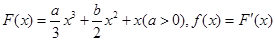 ,若
,若 且对任意实数
且对任意实数 均有
均有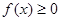 成立.
成立.
(1)求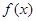 表达式;
表达式;
(2)当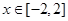 时,
时, 是单调函数,求实数
是单调函数,求实数 的取值范围.
的取值范围.
(本小题满分14分)已知椭圆的中心在原点,焦点在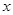 轴上,离心率为
轴上,离心率为 ,且经过点直线
,且经过点直线 ,直线
,直线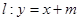 交椭圆于不同的两点
交椭圆于不同的两点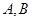 .
.
(1)求椭圆的方程;
(2)求 的取值范围;
的取值范围;
(3)若直线 不过点
不过点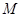 ,求证:直线
,求证:直线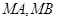 与
与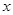 轴围成一个等腰三角形.
轴围成一个等腰三角形.
(本小题满分12分)已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.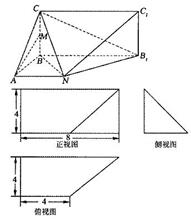
(Ⅰ)若M为CB中点,证明: ;
;
(Ⅱ)求这个几何体的体积.